/Szkoła średnia/Ciągi/Szereg geometryczny/Liczenie sumy

Zadanie nr 5117775

Dodaj do ulubionych
Dodaj do rozwiązanych

Konstruujemy ciąg trójkątów równobocznych 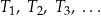T1, T2, T 3, ... następująco:

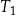  • T1 jest trójkątem równobocznym o polu 1.

  • dla każdego 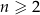n ≥ 2 , trójkąt 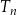Tn ma wierzchołki na trzech różnych bokach trójkąta 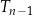Tn−1 i każdy z wierzchołków trójkąta 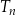Tn dzieli odpowiedni bok trójkąta 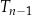Tn −1 w stosunku 1 : 2.

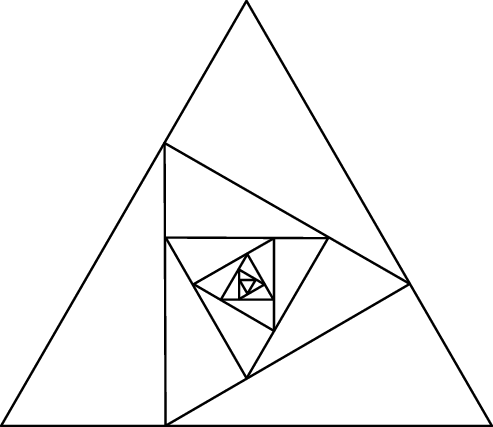
ZINFO-FIGURE

Oblicz sumę pól wszystkich trójkątów 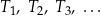T 1, T2, T3, ... .

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.