/Szkoła średnia/Ciągi/Szereg geometryczny/Liczenie sumy

Zadanie nr 7066053

Dodaj do ulubionych
Dodaj do rozwiązanych

W kwadrat o boku a wpisujemy okrąg. W ten okrąg wpisujemy kwadrat, w który wpisujemy okrąg itd. W ten sposób powstanie nieskończony ciąg kwadratów. Oblicz sumę pól wszystkich tych kwadratów.

Rozwiązanie

Zobaczmy jak zmienia się bok kwadratu, przy pojedynczym przejściu.

PIC

Okrąg wpisany w kwadrat ma średnicę a i to jest dokładnie przekątna kolejnego kwadratu. Zatem

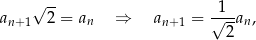
-- a √ 2 = a ⇒ a = √1--a , n+ 1 n n+1 2 n

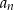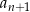gdzie przez an i an+ 1 oznaczyliśmy boki kolejnych kwadratów. Zatem pola tych kwadratów spełniają

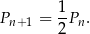
1- Pn+1 = 2Pn .

Musimy więc wysumować szereg geometryczny o pierwszym wyrazie 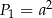P = a2 1 i ilorazie q = 1 2 .

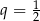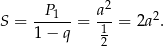
P1 a2 S = ------= -1-= 2a2. 1 − q 2

 
Odpowiedź: 2a2

Wersja PDF