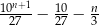/Szkoła średnia/Ciągi/Rekurencyjny/Różne

Zadanie nr 4499198

Dodaj do ulubionych
Dodaj do rozwiązanych

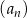Oblicz sumę n początkowych wyrazów ciągu (an) określonego dla 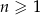n ≥ 1 , w którym

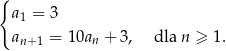
{ a1 = 3 a = 10an + 3, dla n ≥ 1. n+ 1

Rozwiązanie

Zauważmy najpierw, że (korzystamy ze wzoru na sumę kolejnych wyrazów ciągu geometrycznego)

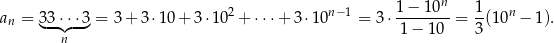
n an = 33 ⋅⋅⋅3 = 3 + 3 ⋅10+ 3 ⋅102 + ⋅⋅⋅+ 3 ⋅10n−1 = 3⋅ 1-−-10-= 1-(10n− 1). ◟--◝n◜-◞ 1− 10 3

Stąd (ponownie korzystamy ze wzoru na sumę kolejnych wyrazów ciągu geometrycznego)

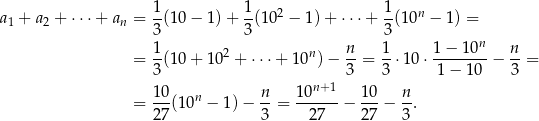
a + a + ⋅⋅⋅+ a = 1(10 − 1) + 1-(102 − 1)+ ⋅⋅⋅+ 1(10n − 1) = 1 2 n 3 3 3 1 2 n n 1 1 − 1 0n n = 3(10 + 10 + ⋅⋅ ⋅+ 10 ) − -3 = 3-⋅1 0⋅-1-−-10-− 3-= n+1 = 10(10n − 1)− n-= 10----− 10-− n-. 27 3 27 27 3

 
Odpowiedź: 10n+1 10 n 27 − 27 − 3

Wersja PDF