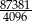/Szkoła średnia/Ciągi/Rekurencyjny/Różne

Zadanie nr 6382039

Dany jest ciąg 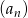(an) określony rekurencyjnie

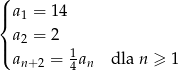
( |{ a1 = 14 a2 = 2 |( 1 an+2 = 4an dla n ≥ 1

Oblicz sumę 18 początkowych wyrazów ciągu 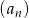(an) .

Wersja PDF

Rozwiązanie

Obliczmy kilka początkowych wyrazów ciągu 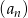(an) .

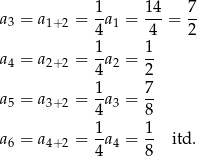
1 14 7 a 3 = a1+2 = --a1 = ---= -- 4 4 2 a = a = 1-a = 1- 4 2+2 4 2 2 1 7 a 5 = a3+2 = 4-a3 = 8- a 6 = a4+2 = 1-a4 = 1- itd. 4 8

Powinno być teraz jasne, że wyrazy ciągu tworzą dwa ciągi geometryczne

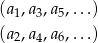
(a1,a3,a5,...) (a2,a4,a6,...)

o wspólnym ilorazie 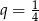q = 1 4 . W takim razie suma 18 początkowych wyrazów ciągu 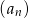(a ) n jest równa

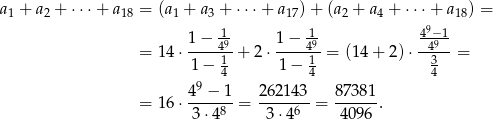
a1 + a2 + ⋅⋅⋅+ a18 = (a1 + a3 + ⋅ ⋅⋅+ a17)+ (a2 + a4 + ⋅⋅⋅+ a18) = 9 1−--149- 1−--149- -4−491 = 14⋅ 1 + 2 ⋅ 1 = (14 + 2 )⋅ 3 = 1 − 4 1 − 4 4 49 −-1- 262143- 8738-1 = 16⋅ 3 ⋅48 = 3⋅46 = 4096 .

 
Odpowiedź: 874308961

Wersja PDF