/Szkoła średnia/Nierówności/Z wartością bezwzględną

Zadanie nr 1717184

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 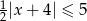1 2 |x + 4| ≤ 5 .

Rozwiązanie

Sposób I

Korzystamy z własności wartości bezwzględnej:

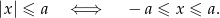
|x| ≤ a ⇐ ⇒ − a ≤ x ≤ a .

W naszej sytuacji mamy

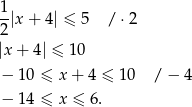
1 -|x + 4| ≤ 5 /⋅ 2 2 |x + 4 | ≤ 1 0 − 10 ≤ x + 4 ≤ 10 / − 4 − 14 ≤ x ≤ 6.

Sposób II

Jak poprzednio, zapisujemy nierówność w postaci

|x + 4 | ≤ 1 0.

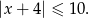
Tym razem rozważmy jednak dwa przypadki (korzystamy z definicji wartości bezwzględnej).
Jeżeli 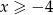x ≥ − 4 to mamy nierówność

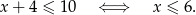
x + 4 ≤ 10 ⇐ ⇒ x ≤ 6.

W połączeniu z założeniem 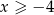x ≥ −4 daje to nam przedział ⟨− 4,6⟩ .
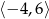Jeżeli natomiast 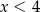x < 4 to mamy nierówność

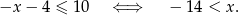
−x − 4 ≤ 10 ⇐ ⇒ − 14 < x.

W połączeniu z założeniem 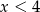x < 4 daje to nam przedział ⟨− 14,4) .
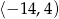Łącząc oba przypadki mamy rozwiązanie: 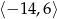⟨−1 4,6⟩ .  
Odpowiedź: ⟨− 14,6⟩

Wersja PDF