/Szkoła średnia/Nierówności/Z wartością bezwzględną

Zadanie nr 2091482

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 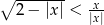∘ ------- x-- 2− |x| < |x| .

Rozwiązanie

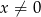Ze względu na x w mianowniku, musimy mieć x ⁄= 0 . Ze względu na pierwiastek, mamy

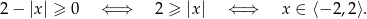
2− |x | ≥ 0 ⇐ ⇒ 2 ≥ |x| ⇐ ⇒ x ∈ ⟨− 2,2 ⟩.

Zauważmy ponadto, że jeżeli 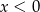x < 0 to prawa strona jest ujemna, a lewa dodatnia, czyli nierówność jest sprzeczna. Podsumowując, możemy założyć, że 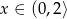x ∈ (0 ,2⟩ . Przy tym założeniu obie strony nierówności są dodatnie i możemy nierówność podnieść stronami do kwadratu.

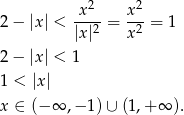
x2 x2 2 − |x| < ---- = ---= 1 |x|2 x2 2 − |x| < 1 1 < |x | x ∈ (−∞ ,− 1) ∪ (1,+ ∞ ).

Uwzględniając nasze wcześniejsze założenie, otrzymujemy

x ∈ (1,2⟩.

 
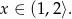
Odpowiedź: (1,2⟩

Wersja PDF