/Szkoła średnia/Nierówności/Z wartością bezwzględną

Zadanie nr 3792561

Dodaj do ulubionych
Dodaj do rozwiązanych

Zaznacz na płaszczyźnie zbiór 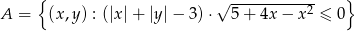{ √ ----------2- } A = (x,y) : (|x|+ |y|− 3) ⋅ 5 + 4x − x ≤ 0 .

Rozwiązanie

Oczywiście pierwiastek jest zawsze nieujemny, więc w zasadzie możemy nie zwracać na niego uwagi. W zasadzie, bo musimy sprawdzić kiedy wyrażanie pod pierwiastkiem jest nieujemne.

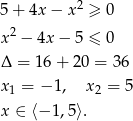
5+ 4x − x2 ≥ 0 2 x − 4x − 5 ≤ 0 Δ = 16+ 20 = 36 x1 = − 1, x2 = 5 x ∈ ⟨− 1,5⟩.

Pozostało nam jeszcze rozszyfrowanie nierówności 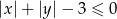|x|+ |y|− 3 ≤ 0 . Rozpiszmy wartość bezwzględną. Jeżeli 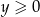y ≥ 0 to mamy nierówność

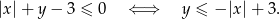
|x |+ y − 3 ≤ 0 ⇐ ⇒ y ≤ − |x|+ 3.

Jeżeli natomiast jeżeli 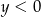y < 0 to mamy

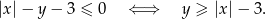
|x |− y − 3 ≤ 0 ⇐ ⇒ y ≥ |x|− 3.

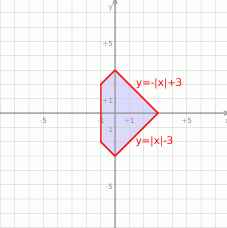
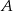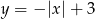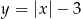Jak teraz narysować zbiór A ? Rysujemy wykresy funkcji y = − |x |+ 3 i y = |x |− 3 pamiętając o tym, że rysujemy tylko ten kawałek pierwszego, który jest powyżej osi 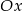Ox . W przypadku drugiego, rysujemy tylko kawałek, który jest poniżej osi 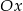Ox . Na koniec trzeba jeszcze sobie przypomnieć, że mamy ograniczenie 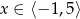x ∈ ⟨− 1,5⟩ (obcinamy wykresy funkcji do tego przedziału). Zbiór 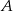A jest zawarty pomiędzy narysowanymi wykresami.

PIC

Wersja PDF