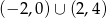/Szkoła średnia/Nierówności/Z wartością bezwzględną

Zadanie nr 3853705

Stosując własności wartości bezwzględnej rozwiąż nierówność: 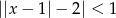||x− 1|− 2 | < 1 .

Wersja PDF

Rozwiązanie

Sposób I

Liczymy

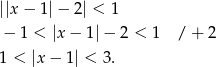
||x− 1|− 2| < 1 − 1 < |x − 1|− 2 < 1 / + 2 1 < |x − 1| < 3.

Lewa nierówność jest równoważna nierównościom

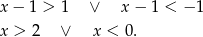
x − 1 > 1 ∨ x− 1 < − 1 x > 2 ∨ x < 0.

Rozwiążmy jeszcze prawą nierówność

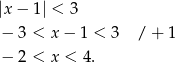
|x− 1| < 3 − 3 < x − 1 < 3 / + 1 − 2 < x < 4 .

Częścią wspólną otrzymanych rozwiązań jest zbiór

(− 2,0) ∪ (2,4).

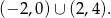
Sposób II

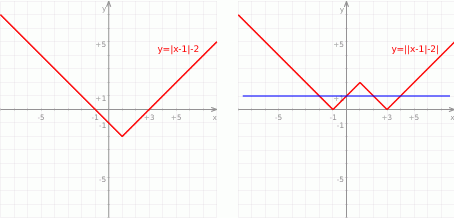
Zadanie możemy też łatwo rozwiązać geometrycznie. Rysujemy najpierw wykres funkcji 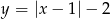y = |x − 1|− 2 – jest to wykres 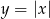y = |x| przesunięty o 1 jednostkę w prawo i o dwie jednostki w dół (czyli o wektor [1,− 2] ).

PIC

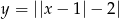Następnie odbijamy część pod osią Ox do góry i mamy wykres funkcji y = ||x − 1|− 2| . Teraz wystarczy odczytać kiedy wykres ten jest poniżej prostej y = 1 .  
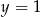Odpowiedź: (− 2,0) ∪ (2,4)

Wersja PDF