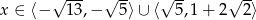Zadanie nr 4187278
Rozwiąż nierówność 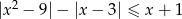 .
.
Rozwiązanie
Jeżeli zapiszemy nierówność w postaci
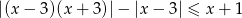
to widać, że do rozpatrzenia mamy 3 przypadki.
Jeżeli 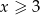 to mamy nierówność
to mamy nierówność
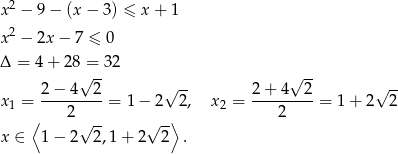
Ponieważ 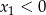 i
i 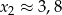 , w połączeniu z warunkiem
, w połączeniu z warunkiem 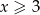 otrzymujemy w tym przypadku
otrzymujemy w tym przypadku 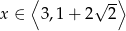 .
.
Jeżeli 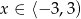 to mamy nierówność
to mamy nierówność
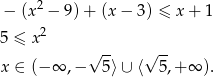
W połączeniu z warunkiem 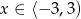 otrzymujemy w tym przypadku
otrzymujemy w tym przypadku
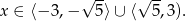
Jeżeli wreszcie 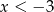 to mamy nierówność
to mamy nierówność
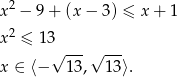
W połączeniu z warunkiem 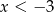 otrzymujemy w tym przypadku
otrzymujemy w tym przypadku 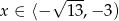 .
.
Łącząc otrzymane rozwiązania otrzymujemy
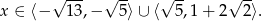
Odpowiedź: