Zadanie nr 5579762
Rozwiąż nierówność 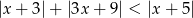 .
.
Rozwiązanie
Sposób I
Aby opuścić wartości bezwzględne, musimy wiedzieć jaki jest znak zawartych w nich wyrażeń. Pierwsze dwa są ujemne dla 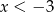 , a trzecie dla
, a trzecie dla 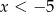 . Zatem dana nierówność prowadzi do nierówności
. Zatem dana nierówność prowadzi do nierówności
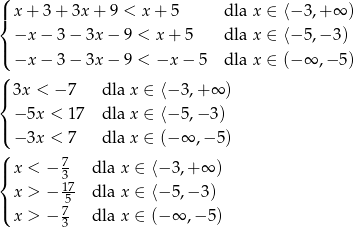
Rozwiązaniem tych nierówności jest zbiór
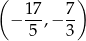
(z pierwszej nierówności mamy 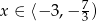 , z drugiej
, z drugiej 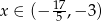 , a trzecia nie ma rozwiązań).
, a trzecia nie ma rozwiązań).
Sposób II
Ponieważ
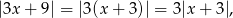
to podaną nierówność możemy zapisać w postaci
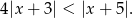
Geometrycznie nierówność ta oznacza, że odległość  od -5 ma być większa niż 4 odległości od -3. Punkty, w których
od -5 ma być większa niż 4 odległości od -3. Punkty, w których 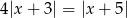 to rozwiązania równań
to rozwiązania równań
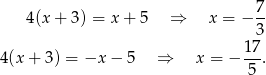
Jeżeli zaznaczymy te punkty na osi, to można zauważyć, że 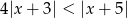 w przedziale
w przedziale 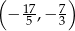 (na zewnątrz tego przedziału odległość
(na zewnątrz tego przedziału odległość  od -5 robi się mniejsza niż
od -5 robi się mniejsza niż 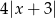 ).
).
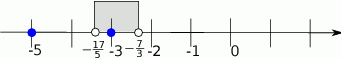
Sposób III
Tak jak poprzednio zauważamy, że podana nierówność jest równoważna nierówności
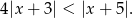
Tym razem jednak nic nie rysujemy, tylko podnosimy nierówność stronami do kwadratu (obie strony są nieujemne!)
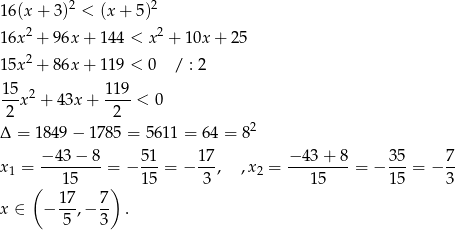
Odpowiedź: