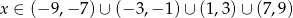Zadanie nr 5850188
Rozwiąż nierówność 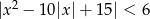 .
.
Rozwiązanie
Sposób I
Nierówność możemy zapisać w postaci
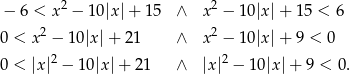
Podstawiamy teraz 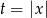 .
.
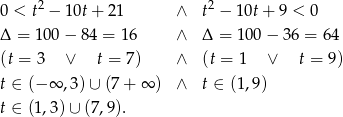
Wracając do  -a.
-a.
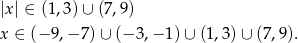
Sposób II
Jak poprzednio zapiszmy nierówność w postaci
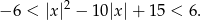
Narysujemy teraz funkcję, która jest w środku. Rysujemy kawałek paraboli 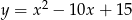 , który jest na prawo od osi
, który jest na prawo od osi 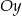 i odbijamy względem osi
i odbijamy względem osi 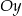 – to jest dokładnie wykres funkcji
– to jest dokładnie wykres funkcji 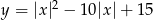 .
.
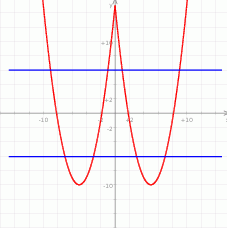
Patrzymy kiedy (dla jakich  -ów) wykres ten jest pomiędzy prostymi
-ów) wykres ten jest pomiędzy prostymi 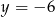 i
i 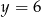 . Otrzymane wartości krańcowe
. Otrzymane wartości krańcowe 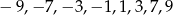 można sprawdzić wstawiając do wzoru i sprawdzając, że wychodzi
można sprawdzić wstawiając do wzoru i sprawdzając, że wychodzi 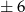 .
.
Odpowiedź: