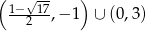Zadanie nr 6429465
Rozwiąż nierówność 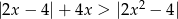 .
.
Rozwiązanie
Wyrażenie pod pierwszą wartością bezwzględną jest dodatnie dla 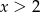 , a wyrażenie pod drugą wartością bezwzględną dla
, a wyrażenie pod drugą wartością bezwzględną dla 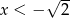 i
i 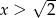 . Mamy zatem możliwe przypadki.
. Mamy zatem możliwe przypadki.
Jeżeli 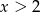 to mamy nierówność
to mamy nierówność
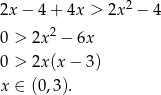
Mamy więc w tym przypadku zbiór rozwiązań: 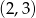 .
.
Jeżeli 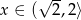 to mamy nierówność
to mamy nierówność
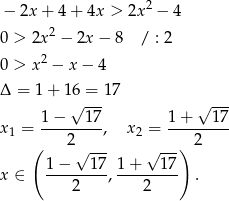
Ponieważ 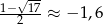 i
i 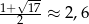 mamy w tym przypadku zbiór rozwiązań:
mamy w tym przypadku zbiór rozwiązań: 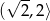 .
.
Jeżeli 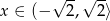 to mamy nierówność
to mamy nierówność
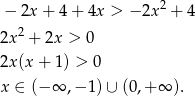
Mamy więc w tym przypadku zbiór rozwiązań: 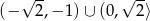 .
.
Jeżeli wreszcie 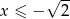 to mamy nierówność
to mamy nierówność
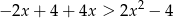
Zauważmy, że jest to dokładnie ta sama nierówność, którą rozwiązywaliśmy w przypadku 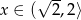 i jej rozwiązaniem jest przedział
i jej rozwiązaniem jest przedział 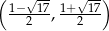 . Mamy więc w tym przypadku zbiór rozwiązań:
. Mamy więc w tym przypadku zbiór rozwiązań: 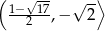 .
.
Łącząc wszystkie otrzymane rozwiązania mamy zbiór rozwiązań:
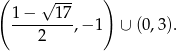
Odpowiedź: