/Szkoła średnia/Nierówności/Z wartością bezwzględną

Zadanie nr 7767426

Rozwiąż nierówność 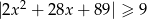2 |2x + 28x + 8 9| ≥ 9 .

Wersja PDF

Rozwiązanie

Aby zobaczyć co jest grane, naszkicujemy wykres lewej strony. Wykresem będzie parabola o ramionach skierowanych w górę i wierzchołku w punkcie

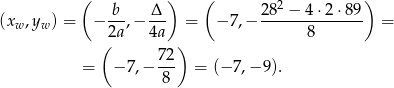
( ) ( ) b-- -Δ- 282 −-4⋅2-⋅89- (xw ,yw ) = − 2a,− 4a = −7 ,− 8 = ( ) = − 7 ,− 72- = (− 7,− 9). 8

Szkicujemy wykres 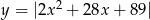y = |2x2 + 28x + 8 9| – pamiętamy o odbiciu części pod osią Ox do góry.

PIC

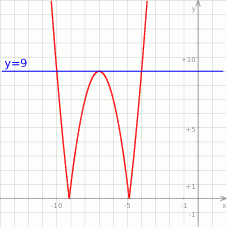
Z obrazka widać już jak będzie wyglądać rozwiązanie nierówności, musimy jeszcze jednak wyznaczyć punkty przecięcia paraboli 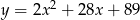y = 2x2 + 28x + 89 z prostą y = 9 .

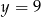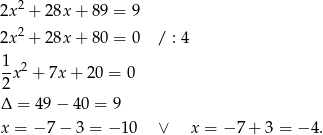
2x2 + 28x + 8 9 = 9 2 2x + 28x + 8 0 = 0 / : 4 1 2 -x + 7x+ 20 = 0 2 Δ = 49− 40 = 9 x = − 7 − 3 = −1 0 ∨ x = − 7 + 3 = − 4.

Zatem rozwiązaniem nierówności jest zbiór

(− ∞ ,− 10⟩∪ { − 7}∪ ⟨−4 ,+∞ ).

 
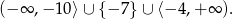
Odpowiedź: x ∈ (− ∞ ,− 10⟩ ∪ {− 7} ∪ ⟨− 4,+ ∞ )

Wersja PDF