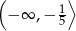/Szkoła średnia/Nierówności/Z wartością bezwzględną

Zadanie nr 8061370

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 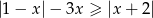|1 − x|− 3x ≥ |x + 2| .

Rozwiązanie

Zapiszmy nierówność w postaci

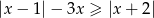
|x − 1|− 3x ≥ |x + 2|

Wyrażenie pod pierwszą wartością bezwzględną zeruje się dla 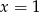x = 1 , a wyrażenie pod drugą dla 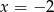x = − 2 , więc mamy do rozpatrzenia 3 przypadki.
Jeżeli 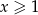x ≥ 1 to mamy nierówność

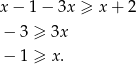
x− 1− 3x ≥ x + 2 − 3 ≥ 3x − 1 ≥ x.

Otrzymane rozwiązanie jest sprzeczne z założeniem 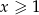x ≥ 1 .
Jeżeli 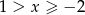1 > x ≥ − 2 to mamy nierówność

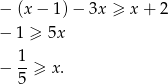
− (x − 1) − 3x ≥ x+ 2 − 1 ≥ 5x 1 − --≥ x. 5

Mamy zatem w tym przypadku 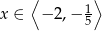⟨ ⟩ x ∈ − 2,− 1 5 .
Jeżeli wreszcie 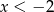x < − 2 to mamy

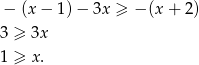
− (x − 1) − 3x ≥ −(x + 2) 3 ≥ 3x 1 ≥ x.

Zatem w tym przypadku 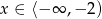x ∈ ⟨− ∞ ,− 2) .
Rozwiązaniem danej nierówności jest więc zbiór

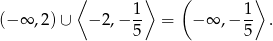
⟨ 1⟩ ( 1⟩ (− ∞ ,2) ∪ − 2 ,− -- = − ∞ ,− -- . 5 5

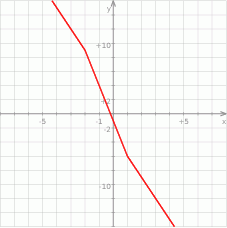
Na koniec, dla ciekawskich, wykres funkcji 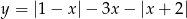y = |1 − x| − 3x − |x + 2| .

PIC

 
Odpowiedź: ( ⟩ − ∞ ,− 15

Wersja PDF