Zadanie nr 8085030
Wyznacz wszystkie wartości parametru 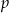 , dla których nierówność
, dla których nierówność 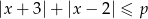 nie ma rozwiązań.
nie ma rozwiązań.
Rozwiązanie
Sposób I
Zauważmy, że wyrażenia 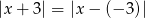 i
i 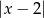 to są dokładnie odległości liczby
to są dokładnie odległości liczby  na osi liczbowej od odpowiednio liczb -3 i 2. Jeżeli myślimy o tym w ten sposób, to widać, że są dwie zasadniczo różne sytuacje.
na osi liczbowej od odpowiednio liczb -3 i 2. Jeżeli myślimy o tym w ten sposób, to widać, że są dwie zasadniczo różne sytuacje.
Jeżeli 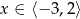 , to mamy
, to mamy
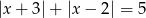
(odczytujemy to z obrazka, jest to po prostu długość przedziału 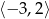 ).
).
Jeżeli natomiast 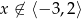 to
to
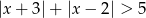
(odległość od przynajmniej jednego końca jest większa niż długość przedziału 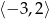 ).
).
W takim razie wiemy, że najmniejsza możliwa wartości wyrażenia 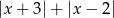 to 5. To oznacza, że nierówność
to 5. To oznacza, że nierówność
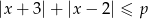
będzie miała rozwiązanie tylko dla 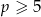 . Zatem nie ma rozwiązań dla
. Zatem nie ma rozwiązań dla 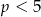 .
.
Sposób II
Tym razem narysujmy wykres funkcji
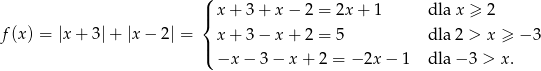
Bez trudu rysujemy wykres.
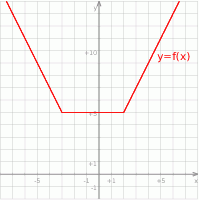
Z wykresu widać, że podana nierówność nie ma rozwiązań dla 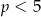 .
.
Odpowiedź: