/Szkoła średnia/Nierówności/Z wartością bezwzględną

Zadanie nr 8703171

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 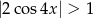|2co s4x| > 1 .

Rozwiązanie

Daną nierówność możemy zapisać w postaci

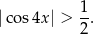
1 |co s4x| > -. 2

Na razie nie zwracajmy uwagi na to, że pod cosinusem jest 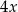4x i naszkicujmy wykres funkcji 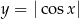y = |cos x| – najpierw rysujemy 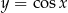y = cos x , potem odbijamy część poniżej osi 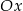Ox do góry.

PIC

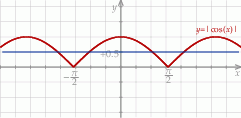
Z obrazka widać, że rozwiązaniem nierówności 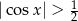|cosx | > 12 jest suma przedziałów postaci

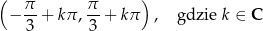
( π π ) − -- + kπ ,--+ kπ , gdzie k ∈ C 3 3

My jednak mamy rozwiązać nierówność 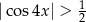1 |cos4x | > 2 , czyli

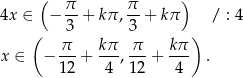
( π π ) 4x ∈ − 3-+ kπ ,3-+ kπ / : 4 ( ) x ∈ − -π-+ kπ-, π-+ kπ- . 12 4 12 4

 
Odpowiedź: ( ) x ∈ − π-+ kπ,-π + kπ- , k ∈ C 12 4 12 4

Wersja PDF