/Szkoła średnia/Nierówności/Z wartością bezwzględną

Zadanie nr 8999879

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 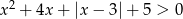2 x + 4x + |x − 3| + 5 > 0 .

Rozwiązanie

Sposób I

Rozważamy dwa przypadki

Jeżeli 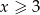x ≥ 3 to mamy nierówność

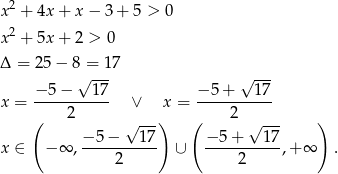
x2 + 4x + x − 3 + 5 > 0 2 x + 5x + 2 > 0 Δ = 25− 8 = 17 √ --- √ --- x = −5-−---1-7- ∨ x = −-5+----17- ( 2 ) ( 2 ) √ --- √ --- x ∈ − ∞ , −-5-−--17- ∪ −-5+----17,+ ∞ . 2 2

Ponieważ oba te pierwiastki są ujemne, uwzględniając nierówność 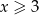x ≥ 3 dostajemy x ∈ ⟨3 ,+ ∞ ) .

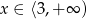Jeżeli 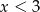x < 3 to mamy nierówność

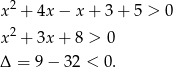
2 x + 4x − x + 3 + 5 > 0 x2 + 3x + 8 > 0 Δ = 9− 32 < 0.

Zatem nierówność ta jest zawsze spełniona.

Sposób II

Jeżeli zapiszemy nierówność w postaci

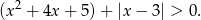
2 (x + 4x + 5) + |x − 3| > 0.

Licząc 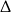Δ -ę trójmianu w pierwszym nawiasie łatwo stwierdzamy, że jest on zawsze dodatni. Drugie wyrażenie jest nieujemne, więc całość jest zawsze dodatnia.  
Odpowiedź: x ∈ R

Wersja PDF