/Szkoła średnia/Nierówności/Z wartością bezwzględną

Zadanie nr 9886535

Dodaj do ulubionych
Dodaj do rozwiązanych

Narysuj w układzie współrzędnych zbiór punktów spełniających nierówność:

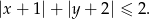
|x + 1| + |y+ 2| ≤ 2.

Rozwiązanie

Rozważmy dwa przypadki.

Jeżeli 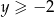y ≥ − 2 to mamy nierówność

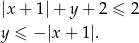
|x + 1| + y + 2 ≤ 2 y ≤ − |x + 1|.

Szkicujemy teraz wykres funkcji 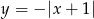y = − |x + 1| i zaznaczamy wszystkie punkty, które jednocześnie leżą pod tym wykresem i nad prostą y = − 2 .

PIC

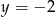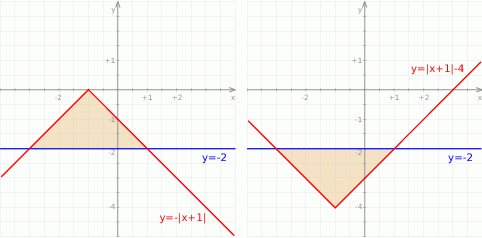
Jeżeli natomiast 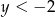y < − 2 to mamy nierówność

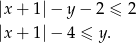
|x + 1| − y − 2 ≤ 2 |x + 1| − 4 ≤ y.

Teraz szkicujemy wykres funkcji 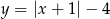y = |x + 1| − 4 i zaznaczamy punkty, które jednocześnie leżą na tym wykresem i pod prostą y = − 2 .

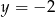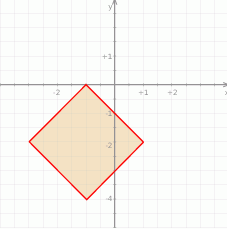
Łącząc oba otrzymane zbiory punktów otrzymujemy następujący kwadrat (łącznie z brzegiem):

PIC

Wersja PDF