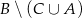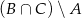- Zaznacz na osi liczbowej i zapisz w postaci przedziału zbiór wszystkich liczb rzeczywistych, których odległość na osi liczbowej od liczby (-1) jest nie większa niż 4.
- Liczba 6,5 stanowi 175% liczby
 . Sprawdź czy liczba
. Sprawdź czy liczba  należy do danego przedziału.
należy do danego przedziału.
/Szkoła średnia/Liczby/Oś liczbowa
Wyznacz algebraicznie zbiór tych wszystkich punktów 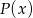 osi liczbowej, których suma odległości od punktów
osi liczbowej, których suma odległości od punktów 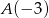 oraz
oraz 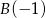 jest mniejsza od 5.
jest mniejsza od 5.
Na osi liczbowej zaznaczono przedział 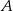 złożony z tych liczb rzeczywistych, których odległość od punktu 1 jest niewiększa od 4,5. Przedział
złożony z tych liczb rzeczywistych, których odległość od punktu 1 jest niewiększa od 4,5. Przedział 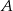 przesunięto wzdłuż osi o 2 jednostki w kierunku dodatnim, otrzymując przedział
przesunięto wzdłuż osi o 2 jednostki w kierunku dodatnim, otrzymując przedział 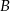 . Wyznacz wszystkie liczby całkowite, które należą jednocześnie do
. Wyznacz wszystkie liczby całkowite, które należą jednocześnie do 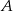 i do
i do 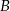 .
.
Zbiór 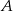 jest zbiorem liczb rzeczywistych, których odległość na osi liczbowej od (-3) jest większa niż 2. Zbiór
jest zbiorem liczb rzeczywistych, których odległość na osi liczbowej od (-3) jest większa niż 2. Zbiór 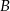 jest przedstawiony na osi liczbowej.
jest przedstawiony na osi liczbowej.
![]()
- Opisz zbiory
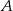 i
i 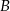 za pomocą nierówności z wartością bezwzględną.
za pomocą nierówności z wartością bezwzględną. - Podaj przykład liczby niewymiernej, która należy jednocześnie do zbioru
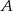 i do zbioru
i do zbioru 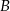 .
.
Przybliżenie z nadmiarem liczby  jest równe 15, a błąd względny tego przybliżenia wynosi 0,025. Wyznacz liczbę
jest równe 15, a błąd względny tego przybliżenia wynosi 0,025. Wyznacz liczbę  .
.
Przybliżenie z niedomiarem liczby  jest równe 12, a błąd względny tego przybliżenia wynosi 0,0125. Wyznacz liczbę
jest równe 12, a błąd względny tego przybliżenia wynosi 0,0125. Wyznacz liczbę  .
.
Niech 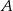 będzie zbiorem rozwiązań równania
będzie zbiorem rozwiązań równania 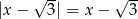 ,
, 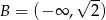 oraz
oraz 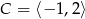 . Wyznacz zbiór
. Wyznacz zbiór 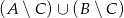 .
.
Zaznacz na osi liczbowej przedziały 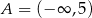 i
i 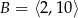 . Wyznacz
. Wyznacz 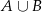 ,
, 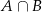 ,
, 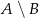 i
i 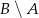 .
.
Zaznacz na osi liczbowej przedziały 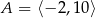 i
i 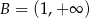 . Wyznacz
. Wyznacz 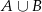 ,
, 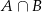 ,
, 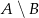 i
i 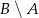 .
.
Wiadomo, że 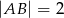 i
i 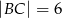 . Znajdź warunek, jaki musi spełniać odległość
. Znajdź warunek, jaki musi spełniać odległość 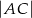 , aby punkty
, aby punkty 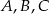 były współliniowe.
były współliniowe.
Niech 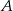 będzie zbiorem wszystkich liczb
będzie zbiorem wszystkich liczb  , które spełniają równość
, które spełniają równość 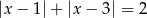 . Niech
. Niech 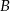 będzie zbiorem wszystkich punktów na osi liczbowej, których suma odległości od punktów 4 i 6 jest niewiększa niż 4. Zaznacz na osi liczbowej zbiory
będzie zbiorem wszystkich punktów na osi liczbowej, których suma odległości od punktów 4 i 6 jest niewiększa niż 4. Zaznacz na osi liczbowej zbiory 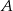 i
i 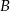 oraz wszystkie punkty, które należą jednocześnie do
oraz wszystkie punkty, które należą jednocześnie do 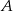 i do
i do 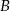 .
.
Niech 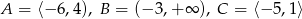 . Wyznacz zbiór
. Wyznacz zbiór 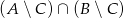 .
.
Dane są zbiory: 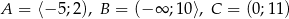 . Zapisz w postaci przedziału lub sumy przedziałów zbiory:
. Zapisz w postaci przedziału lub sumy przedziałów zbiory: