/Szkoła średnia/Równania

Zadanie nr 1008135

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie

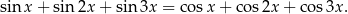
sinx + sin 2x + sin3x = cosx + cos2x + co s3x.

Rozwiązanie

Korzystamy ze wzorów na sumę sinusów i sumę cosinusów.

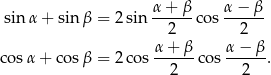
α + β α − β sinα + sin β = 2 sin ------co s------ 2 2 co sα + cos β = 2 cos α+--β-cos α-−-β-. 2 2

Przekształcamy dane równanie.

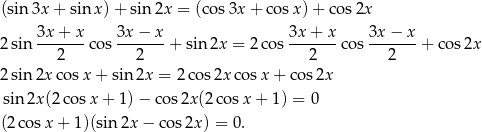
(sin 3x + sin x)+ sin 2x = (cos3x + c osx) + cos 2x 3x + x 3x − x 3x + x 3x− x 2sin ---2---cos ---2---+ sin 2x = 2 cos --2----cos --2----+ cos 2x 2sin 2x cosx + sin 2x = 2 cos2x cos x+ cos2x sin 2x(2c osx + 1) − cos 2x(2 cosx + 1) = 0 (2co sx + 1)(sin2x − cos2x ) = 0.

Wyrażenie w pierwszym nawiasie zeruje się gdy 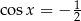cos x = − 1 2 . Szkicujemy cosinusa

PIC

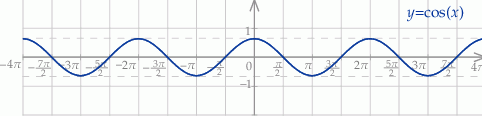
i odczytujemy rozwiązanie

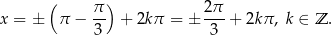
( ) x = ± π − π- + 2kπ = ± 2π- + 2kπ , k ∈ Z . 3 3

Wyrażenie w drugim nawiasie zeruje się gdy

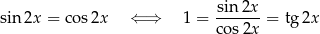
sin2x sin2x = cos 2x ⇐ ⇒ 1 = -------= tg 2x cos2x

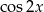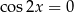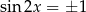(możemy podzielić przez cos2x , bo jeżeli cos 2x = 0 , to sin 2x = ± 1 i taka liczba x na pewno nie spełnia powyższego równania). Szkicujemy tangensa

PIC

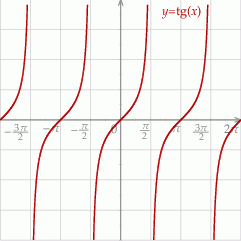
Mamy zatem

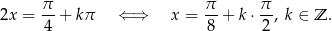
π π π 2x = --+ kπ ⇐ ⇒ x = -- + k ⋅--, k ∈ Z . 4 8 2

 
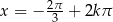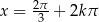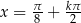Odpowiedź: 2π- x = − 3 + 2kπ lub 2π- x = 3 + 2kπ lub x = π8-+ kπ2- , k ∈ Z

Wersja PDF