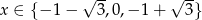Zadanie nr 1056202
Rozwiąż równanie 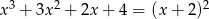 .
.
Rozwiązanie
Liczymy
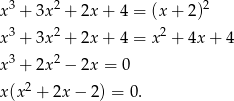
Zatem jednym pierwiastkiem jest 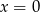 . Aby znaleźć pozostałe rozkładamy trójmian w nawiasie.
. Aby znaleźć pozostałe rozkładamy trójmian w nawiasie.
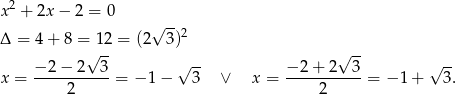
Odpowiedź: 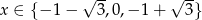
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 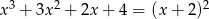 .
.
Liczymy
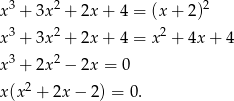
Zatem jednym pierwiastkiem jest 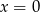 . Aby znaleźć pozostałe rozkładamy trójmian w nawiasie.
. Aby znaleźć pozostałe rozkładamy trójmian w nawiasie.
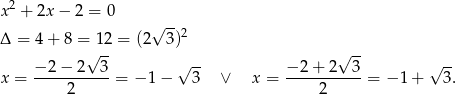
Odpowiedź: