/Szkoła średnia/Równania

Zadanie nr 1113005

Wyznacz wszystkie liczby rzeczywiste 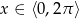x ∈ ⟨0,2π ⟩ , dla których

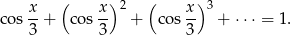
x ( x )2 ( x )3 cos --+ cos-- + cos-- + ⋅⋅⋅ = 1. 3 3 3
Wersja PDF

Rozwiązanie

Lewa strona równania jest sumą szeregu geometrycznego o ilorazie 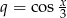x q = cos 3 . Taki szereg jest zbieżny jeżeli 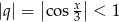| | |q| = |cos x3| < 1 , czyli 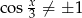cos x3 ⁄= ± 1 . Przy tym założeniu możemy równanie zapisać w postaci

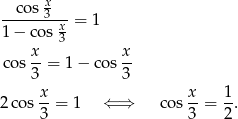
x --cos-3-- 1 − cos x = 1 x 3 x cos --= 1− cos-- 3 3 2cos x-= 1 ⇐ ⇒ cos x = 1-. 3 3 2

Szkicujemy teraz cosinusa.

PIC

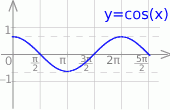
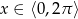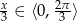Teraz trzeba uważać, bo x ∈ ⟨0,2π ⟩ , ale x3 ∈ ⟨0, 2π3 ⟩ . To oznacza, że równanie ma tylko jedno rozwiązanie

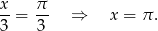
x π --= -- ⇒ x = π. 3 3

 
Odpowiedź: x = π

Wersja PDF