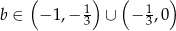/Szkoła średnia/Równania

Zadanie nr 1187357

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 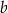b , dla których równanie 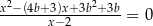2 2 x-−-(4b+3)x+3b-+3b = 0 x− 2 ma dwa rozwiązania różnych znaków.

Rozwiązanie

Zauważmy, że 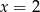x = 2 nie należy do dziedziny danego równania – będziemy musieli o tym pamiętać ustalając ilość rozwiązań.

Mnożąc przez mianownik otrzymujemy równanie

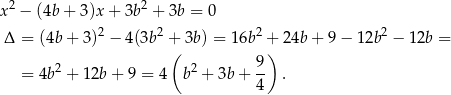
x2 − (4b + 3)x + 3b2 + 3b = 0 2 2 2 2 Δ = (4b + 3) − 4(3b +( 3b ) = 16b +) 24b + 9 − 12b − 12b = 2 2 9- = 4b + 12b + 9 = 4 b + 3b + 4 .

Aby równanie miało dwa pierwiastki musi być 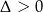Δ > 0

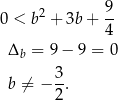
0 < b2 + 3b + 9- 4 Δb = 9− 9 = 0 b ⁄= − 3-. 2

Sprawdźmy jeszcze kiedy 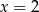x = 2 jest pierwiastkiem – musimy ten przypadek wykluczyć.

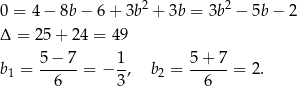
2 2 0 = 4− 8b− 6+ 3b + 3b = 3b − 5b − 2 Δ = 25 + 2 4 = 49 b1 = 5-−-7-= − 1, b2 = 5+--7-= 2. 6 3 6

Zatem równanie ma dwa różne rozwiązania dla 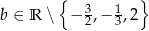{ 3 1 } b ∈ R ∖ − 2,− 3,2 .

Pozostało sprawdzić kiedy rozwiązania są różnych znaków. Tak będzie gdy ich iloczyn jest ujemny, czyli na mocy wzorów Viète’a

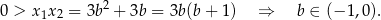
2 0 > x1x2 = 3b + 3b = 3b(b + 1) ⇒ b ∈ (− 1 ,0).

 
Odpowiedź: ( ) ( ) b ∈ − 1,− 13 ∪ − 13,0

Wersja PDF