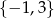/Szkoła średnia/Równania

Zadanie nr 1256669

Rozwiąż równanie 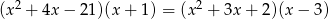2 2 (x + 4x − 21)(x + 1) = (x + 3x+ 2)(x − 3) .

Wersja PDF

Rozwiązanie

Sposób I

Rozpoczynamy od rozłożenia funkcji kwadratowych, które są w nawiasach po obu stronach równania. Najpierw funkcja z lewej strony.

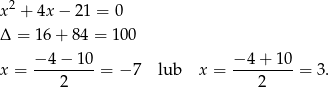
x 2 + 4x − 21 = 0 Δ = 16 + 84 = 100 − 4 − 10 − 4 + 10 x = ---------= − 7 lub x = ---------= 3. 2 2

Teraz funkcja z prawej strony.

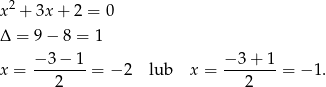
x2 + 3x+ 2 = 0 Δ = 9 − 8 = 1 − 3 − 1 − 3 + 1 x = ------- = − 2 lub x = ------- = − 1. 2 2

Dane równanie możemy więc zapisać w postaci

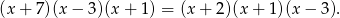
(x+ 7)(x− 3)(x + 1) = (x + 2)(x + 1 )(x− 3).

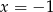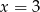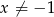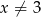Widać teraz, że pierwiastkami równania są x = − 1 i x = 3 . Jeżeli natomiast x ⁄= − 1 i x ⁄= 3 , to powyższe równanie możemy podzielić stronami przez 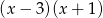(x − 3)(x + 1 ) i otrzymujemy

x + 7 = x + 2.

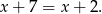
Otrzymane równanie jest sprzeczne, więc nie ma żadnych dodatkowych rozwiązań.

Sposób II

Przekształcamy dane równanie (wymnażamy wyrażenia w nawiasach).

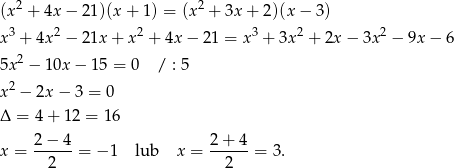
2 2 (x + 4x − 21)(x + 1 ) = (x + 3x + 2)(x − 3) x3 + 4x2 − 21x + x 2 + 4x − 21 = x3 + 3x 2 + 2x − 3x 2 − 9x− 6 5x2 − 10x − 1 5 = 0 / : 5 2 x − 2x − 3 = 0 Δ = 4+ 12 = 16 x = 2−--4-= − 1 lub x = 2+--4-= 3. 2 2

 
Odpowiedź: {− 1,3 }

Wersja PDF