/Szkoła średnia/Równania

Zadanie nr 1312454

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 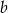b , dla których równanie 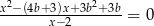2 2 x-−-(4b+3)x+3b-+3b = 0 x− 2 ma

  • jedno rozwiązanie,
  • dwa różne rozwiązania ujemne.

Rozwiązanie

Oczywiście wystarczy zajmować się równaniem kwadratowym w liczniku, pamiętając, że 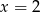x = 2 nie może być pierwiastkiem równania. Od razu sprawdźmy kiedy tak jest (podstawiamy 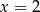x = 2 do równania).

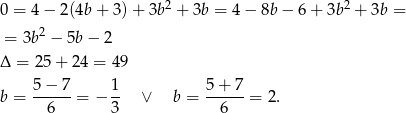
0 = 4− 2 (4b+ 3)+ 3b2 + 3b = 4 − 8b − 6 + 3b2 + 3b = 2 = 3b − 5b − 2 Δ = 25 + 24 = 49 5− 7 1 5 + 7 b = ------= − -- ∨ b = ------= 2. 6 3 6
  • Liczymy 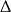Δ -ę.
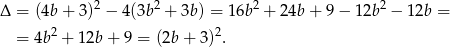
    Δ = (4b+ 3)2 − 4 (3b2 + 3b) = 16b2 + 24b + 9 − 12b 2 − 1 2b = 2 2 = 4b + 12b+ 9 = (2b + 3) .

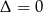    Zatem Δ = 0 (czyli równanie ma jeden pierwiastek) dla 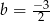b = −23 . Trzeba jeszcze uwzględnić wcześniej rozważoną sytuację, gdy jednym z pierwiastków jest 2 – wtedy równanie też ma tylko jeden pierwiastek.  
    Odpowiedź: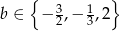 { } b ∈ − 3 ,− 1,2 2 3

  • Z poprzedniego podpunktu wiemy, kiedy równanie ma dwa różne pierwiastki, pozostało sprawdzić kiedy oba są ujemne. Tak będzie gdy ich suma będzie ujemna, a iloczyn dodatni. Na mocy wzorów Viète’a mamy
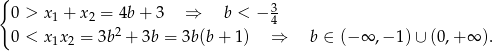
    { 3 0 > x1 + x2 = 4b + 3 ⇒ b < − 4 0 < x1x2 = 3b 2 + 3b = 3b(b + 1) ⇒ b ∈ (− ∞ ,− 1) ∪ (0,+ ∞ ).

    Układ ten daje nam 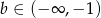b ∈ (− ∞ ,− 1) . Pozostało zauważyć, że z poprzedniego podpunktu wynika, iż z tego zbioru musimy wyrzucić − 32 .  
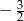    Odpowiedź: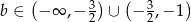 b ∈ (− ∞ ,− 3) ∪ (− 3,− 1) 2 2 .

Wersja PDF