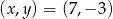Zadanie nr 1334482
Rozwiąż układ równań 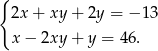
Rozwiązanie
Z pierwszego równania mamy 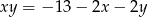 . Wstawiając to do drugiego równania mamy
. Wstawiając to do drugiego równania mamy
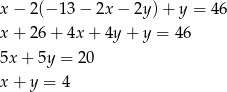
Sposób I
Podstawiamy 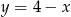 do pierwszego równania.
do pierwszego równania.
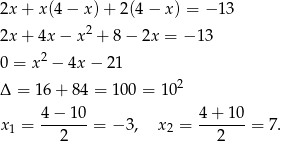
Daje to odpowiednio 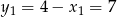 i
i 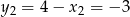 i otrzymujemy dwie pary rozwiązań:
i otrzymujemy dwie pary rozwiązań:
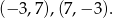
Sposób II
Podstawiając 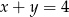 do drugiego równania mamy
do drugiego równania mamy
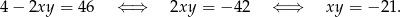
Mamy więc
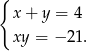
Na mocy wzorów Viète’a rozwiązania tego układu równań są pierwiastkami równania kwadratowego
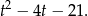
Rozwiązując równanie tak jak poprzednio otrzymamy dwa pierwiastki 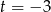 i
i 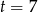 . Zatem
. Zatem 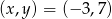 lub
lub 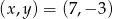 .
.
Odpowiedź: 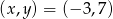 lub
lub