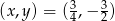Zadanie nr 1387787
Rozwiąż układ równań 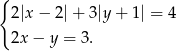
Rozwiązanie
Z drugiego równania możemy wyliczyć 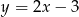 i wstawić do pierwszego równania.
i wstawić do pierwszego równania.
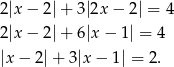
Mamy teraz do rozważenia 3 przypadki
- Jeżeli
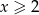 , to mamy równanie
, to mamy równanie 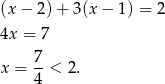
W tym przypadku nie ma więc rozwiązań.
- Jeżeli
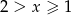 , to mamy równanie
, to mamy równanie 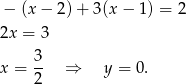
W tym przypadku mamy więc rozwiązanie
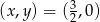 .
. - Jeżeli
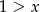 , to mamy równanie
, to mamy równanie 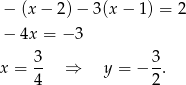
W tym przypadku mamy więc rozwiązanie
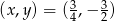 .
.
Odpowiedź: 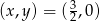 lub
lub