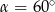Zadanie nr 1676148
Wyznacz miarę kąta ostrego  , dla którego wyrażenie
, dla którego wyrażenie 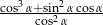 ma wartość 2.
ma wartość 2.
Rozwiązanie
Przekształćmy dane wyrażenie (korzystamy z jedynki trygonometrycznej).
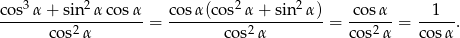
Pozostało rozwiązać równanie
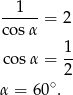
Odpowiedź: 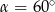
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyznacz miarę kąta ostrego  , dla którego wyrażenie
, dla którego wyrażenie 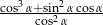 ma wartość 2.
ma wartość 2.
Przekształćmy dane wyrażenie (korzystamy z jedynki trygonometrycznej).
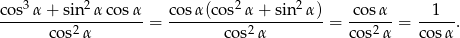
Pozostało rozwiązać równanie
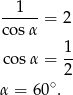
Odpowiedź: