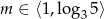/Szkoła średnia/Równania

Zadanie nr 1686184

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz te wartości parametru 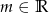m ∈ R , dla których równanie

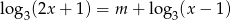
log3(2x + 1) = m + log 3(x− 1)

ma pierwiastek należący do zbioru 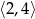⟨2,4⟩ .

Rozwiązanie

Spróbujmy rozwiązać to równanie.

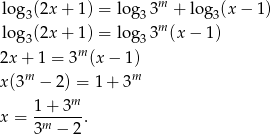
lo g (2x + 1) = log 3m + log (x − 1 ) 3 3 3 lo g3(2x + 1) = log 33m(x − 1) 2x + 1 = 3m(x − 1) m m x (3 − 2) = 1 + 3 1 + 3m x = -m-----. 3 − 2

Oczywiście to wyliczenie ma sens, o ile

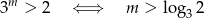
m 3 > 2 ⇐ ⇒ m > log3 2

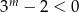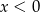(bo jeżeli m 3 − 2 < 0 to x < 0 co jest niemożliwe ze względu na 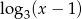log 3(x− 1) w równaniu).

Sprawdźmy kiedy wyliczony pierwiastek jest w podanym przedziale

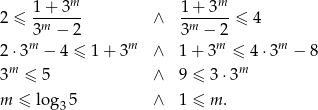
m m 2 ≤ 1+--3-- ∧ 1-+-3--≤ 4 3m − 2 3m − 2 2 ⋅3m − 4 ≤ 1+ 3m ∧ 1+ 3m ≤ 4 ⋅3m − 8 m m 3 ≤ 5 ∧ 9 ≤ 3 ⋅3 m ≤ log 5 ∧ 1 ≤ m . 3

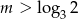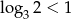Na koniec musimy sobie przypomnieć, że m > lo g32 , ale log 32 < 1 , więc to nic nie zmienia.  
Odpowiedź: m ∈ ⟨1,log35 ⟩

Wersja PDF