/Szkoła średnia/Równania

Zadanie nr 1687026

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 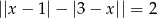||x − 1| − |3− x|| = 2 .

Rozwiązanie

Dane równanie możemy zapisać w postaci

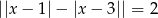
||x − 1|− |x − 3|| = 2

Rozważamy trzy przypadki.
Jeżeli 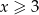x ≥ 3 to mamy równanie

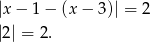
|x − 1 − (x − 3)| = 2 |2| = 2.

Widać zatem, że w tym przypadku równanie jest zawsze spełnione.
Jeżeli 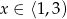x ∈ ⟨1 ,3) to mamy równanie

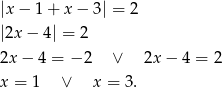
|x− 1+ x− 3| = 2 |2x− 4| = 2 2x − 4 = − 2 ∨ 2x − 4 = 2 x = 1 ∨ x = 3.

Otrzymujemy więc w tym przypadku jedno rozwiązanie: 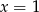x = 1 .
Jeżeli wreszcie 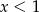x < 1 to mamy równanie

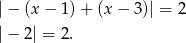
|− (x− 1)+ (x− 3)| = 2 |− 2| = 2.

Zatem w tym przypadku równanie również jest zawsze spełnione.

Podsumowując, zbiór rozwiązań równania jest równy

(− ∞ ,1⟩ ∪ ⟨3,+ ∞ ).

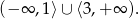
Na koniec (dla ciekawskich) wykres lewej strony równania.

PIC

 
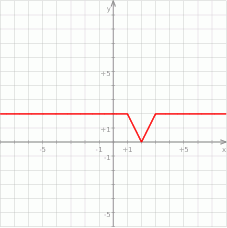
Odpowiedź: (− ∞ ,1⟩ ∪ ⟨3,+ ∞ )

Wersja PDF