Definicja Funkcję określoną wzorem 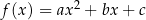 , gdzie
, gdzie 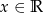 i
i 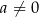 nazywamy funkcją kwadratową. Liczby
nazywamy funkcją kwadratową. Liczby 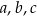 nazywamy współczynnikami funkcji kwadratowej
nazywamy współczynnikami funkcji kwadratowej 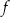 . Wykres funkcji kwadratowej nazywamy parabolą. Postać kanoniczna
. Wykres funkcji kwadratowej nazywamy parabolą. Postać kanoniczna
Twierdzenie 1
Funkcję kwadratową 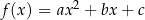 można przedstawić w postaci
można przedstawić w postaci
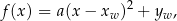
gdzie 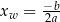 i
i 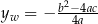 . Postać tę nazywamy postacią kanoniczną funkcji kwadratowej
. Postać tę nazywamy postacią kanoniczną funkcji kwadratowej 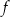 .
.
Dowód Przekształcamy wzór funkcji 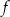 korzystając zez wzoru
korzystając zez wzoru 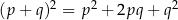 .
.
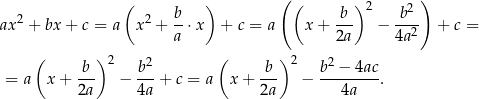
Miejsca zerowe
Twierdzenie 2
Niech 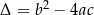 , gdzie
, gdzie 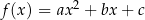 jest funkcją kwadratową. Wtedy równanie
jest funkcją kwadratową. Wtedy równanie 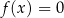
-
nie ma rozwiązań jeżeli
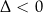 ;
; -
ma jedno rozwiązanie
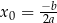 jeżeli
jeżeli 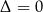 ;
; -
ma dwa rozwiązania
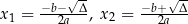 jeżeli
jeżeli 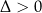 .
.
Liczbę 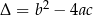 nazywamy wyróżnikiem równania
nazywamy wyróżnikiem równania 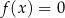 , a samo równanie
, a samo równanie 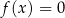 nazywamy równaniem kwadratowym.
nazywamy równaniem kwadratowym.
Dowód Korzystamy z wyprowadzonej wcześniej postaci kanonicznej:
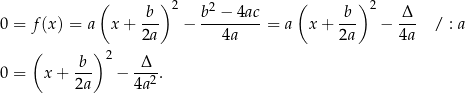
Jeżeli 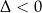 , to prawa strona powyższej równości jest dodatnia, co dowodzi sprzeczności równania w tym przypadku.
, to prawa strona powyższej równości jest dodatnia, co dowodzi sprzeczności równania w tym przypadku.
Jeżeli natomiast 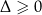 to mamy
to mamy
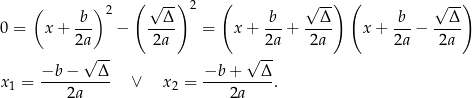
Otrzymane rozwiązania są równe tylko wtedy, gdy 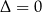 .
.
Śledząc uważnie przekształcenie z powyższego dowodu, otrzymujemy
Wniosek 3
Jeżeli 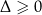 to funkcję kwadratową
to funkcję kwadratową 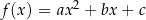 można zapisać w postaci
można zapisać w postaci
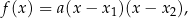
gdzie 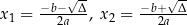 .
.
Jeżeli 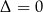 to
to 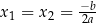 i otrzymujemy rozkład
i otrzymujemy rozkład
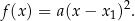
Powyższą postać wzoru funkcji kwadratowej nazywa się postacią iloczynową.
Wzory Viète’a
Twierdzenie 4
Dwie funkcje kwadratowe 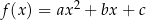 i
i 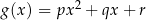 są równe (tzn. przyjmują te same wartości dla dowolnego
są równe (tzn. przyjmują te same wartości dla dowolnego 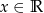 ) wtedy i tylko wtedy gdy
) wtedy i tylko wtedy gdy 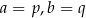 i
i 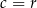 .
.
Dowód Implikacja "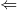 " jest oczywista, więc zajmiemy się implikacją "
" jest oczywista, więc zajmiemy się implikacją "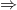 ", czyli zakładamy, że równość
", czyli zakładamy, że równość
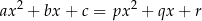
jest spełniona dla dowolnego 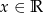 . Podstawiając w tej równości
. Podstawiając w tej równości 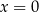 otrzymujemy
otrzymujemy 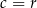 i zostaje nam równość
i zostaje nam równość
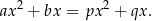
Teraz podstawmy 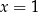 i
i 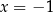 . Da nam to układ równań
. Da nam to układ równań
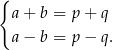
Dodając, a potem odejmując równania stronami, otrzymujemy 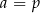 i
i 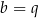 .
.
Twierdzenie 5
Jeżeli 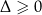 i
i 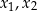 są pierwiastkami równania kwadratowego
są pierwiastkami równania kwadratowego 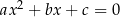 , przy czym przyjmujemy
, przy czym przyjmujemy 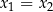 w przypadku
w przypadku 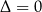 , to prawdziwe są równości
, to prawdziwe są równości
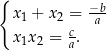
Wzory powyższe noszą nazwę wzorów Viète’a.
Dowód Korzystając z postaci iloczynowej funkcji kwadratowej (Wniosek 3) mamy
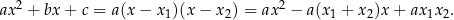
Na mocy Twierdzenia 4, współczynniki po obu stronach tej równości muszą być równe, co daje nam układ
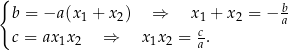
Twierdzenie 6
Jeżeli liczby 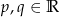 spełniają równości
spełniają równości
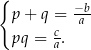
dla pewnych liczb 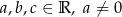 , to liczby
, to liczby 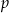 i
i 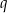 są pierwiastkami równania
są pierwiastkami równania
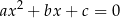
(w szczególności równanie to ma pierwiastki).
Dowód Pomnóżmy obie strony każdego z równań przez  .
.
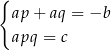
Jeżeli podstawimy teraz z pierwszego równania 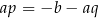 do drugiego, to otrzymamy
do drugiego, to otrzymamy
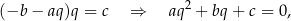
czyli liczba 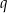 jest rozwiązaniem równania
jest rozwiązaniem równania 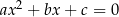 . Podobnie pokazujemy, że liczba
. Podobnie pokazujemy, że liczba 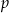 jest pierwiastkiem tego równania.
jest pierwiastkiem tego równania.
Własności paraboli
Lemat 7
Funkcja 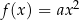 , gdzie
, gdzie 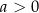 ma następujące własności:
ma następujące własności:
-
Funkcja
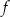 jest parzysta, tzn.
jest parzysta, tzn. 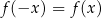 . W szczególności, wykres funkcji
. W szczególności, wykres funkcji 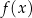 jest symetryczny względem prostej
jest symetryczny względem prostej 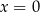 .
. -
Funkcja
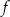 jest malejąca na przedziale
jest malejąca na przedziale 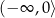 i rosnąca na przedziale
i rosnąca na przedziale 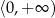 .
. -
Zbiorem wartości funkcji
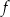 jest przedział
jest przedział 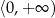 . Ponadto każda liczba
. Ponadto każda liczba 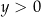 jest wartością funkcji dla dokładnie dwóch argumentów. Wartość 0 jest przyjmowana w dokładnie jednym punkcie:
jest wartością funkcji dla dokładnie dwóch argumentów. Wartość 0 jest przyjmowana w dokładnie jednym punkcie: 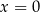 .
. -
Funkcja
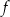 jest funkcją wypukłą, tzn. dla dowolnych liczb
jest funkcją wypukłą, tzn. dla dowolnych liczb 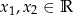 i
i 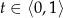 spełniona jest nierówność:
spełniona jest nierówność: 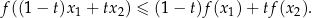
Równość w tej nierówności zachodzi wtedy i tylko wtedy, gdy
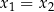 lub
lub 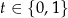 .
.
Dowód
-
Liczymy
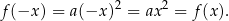
Jeżeli weźmiemy dowolny punkt
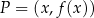 na wykresie funkcji
na wykresie funkcji 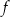 , to na mocy parzystości funkcji
, to na mocy parzystości funkcji 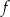 , obraz
, obraz 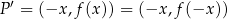 punktu
punktu 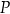 przy symetrii względem prostej
przy symetrii względem prostej 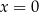 jest również punktem wykresu
jest również punktem wykresu 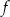 . Wykres jest więc symetryczny względem tej prostej.
. Wykres jest więc symetryczny względem tej prostej. -
Niech
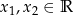 oraz
oraz 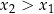 . Zauważmy, że
. Zauważmy, że 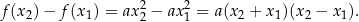
Jeżeli zatem
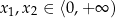 to
to 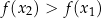 , co dowodzi, że funkcja jest rosnąca na przedziale
, co dowodzi, że funkcja jest rosnąca na przedziale 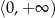 . Jeżeli natomiast
. Jeżeli natomiast 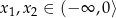 to
to 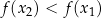 , co oznacza, że funkcja jest malejąca na tym przedziale.
, co oznacza, że funkcja jest malejąca na tym przedziale. -
Niech
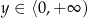 . Mamy wtedy
. Mamy wtedy 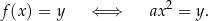
Lewa strona jest liczbą nieujemną, więc widać, że równanie
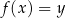 (z niewiadomą
(z niewiadomą  ) nie ma rozwiązań dla
) nie ma rozwiązań dla 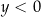 . Jeżeli natomiast
. Jeżeli natomiast 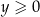 to mamy
to mamy 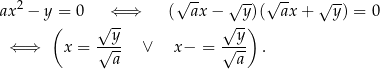
Równanie ma więc zawsze dwa rozwiązania, z wyjątkiem sytuacji
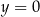 , kiedy rozwiązanie jest jedno.
, kiedy rozwiązanie jest jedno. -
Przekształcamy żądaną nierówność
![f((1− t)x1 + tx 2) ≤ (1− t)f (x1)+ tf(x2) a[(1 − t)x + tx ]2 ≤ (1 − t)ax2+ tax2 / : a 1 2 1 2 (1− t)2x 21 + 2(1 − t)x1tx2 + t2x22 ≤ (1 − t)x21 + tx22 2 2 2 2 0 ≤ (1− t− 1 + 2t − t )x1 − 2t(1− t)x1x2 + (t− t )x2 0 ≤ t(1− t)(x 2− 2x 1x2 + x2) 1 2 2 0 ≤ t(1− t)(x 1 − x 2) .](https://img.zadania.info/por/0021995/HporT117x.png)
Ponieważ
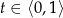 , nierówność ta jest spełniona oraz równość zachodzi tylko dla
, nierówność ta jest spełniona oraz równość zachodzi tylko dla 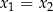 lub
lub 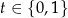 . Dowodzi to wypukłości funkcji
. Dowodzi to wypukłości funkcji 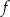 .
.
Twierdzenie 8
Funkcja 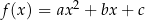 ma następujące własności:
ma następujące własności:
-
Wykres funkcji
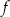 jest symetryczny względem prostej
jest symetryczny względem prostej 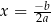 .
. -
Funkcja
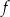 jest malejąca na przedziale
jest malejąca na przedziale 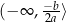 i rosnąca na przedziale
i rosnąca na przedziale 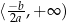 dla
dla 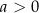 , oraz rosnąca na przedziale
, oraz rosnąca na przedziale 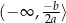 i malejąca na przedziale
i malejąca na przedziale 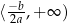 dla
dla 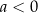 .
. -
Zbiorem wartości funkcji
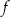 jest przedział
jest przedział 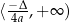 dla
dla 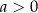 oraz przedział
oraz przedział 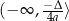 dla
dla 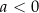 . Ponadto każda liczba
. Ponadto każda liczba 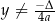 z tego przedziału jest wartością funkcji dla dokładnie dwóch argumentów. Wartość
z tego przedziału jest wartością funkcji dla dokładnie dwóch argumentów. Wartość 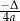 jest przyjmowana w dokładnie jednym punkcie:
jest przyjmowana w dokładnie jednym punkcie: 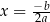 . Punkt o współrzędnych
. Punkt o współrzędnych 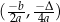 nazywamy wierzchołkiem paraboli
nazywamy wierzchołkiem paraboli 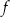 .
. -
Funkcja
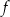 jest funkcją wypukłą dla
jest funkcją wypukłą dla 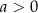 i wklęsłą dla
i wklęsłą dla 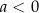 .
.
Dowód Patrząc na postać kanoniczną
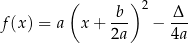
widzimy, że wykres funkcji 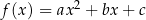 powstaje z wykresu funkcji
powstaje z wykresu funkcji 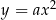 przez przesunięcie o wektor
przez przesunięcie o wektor ![−b −Δ [-2a-,4a-]](https://img.zadania.info/por/0021995/HporT148x.png) .
.
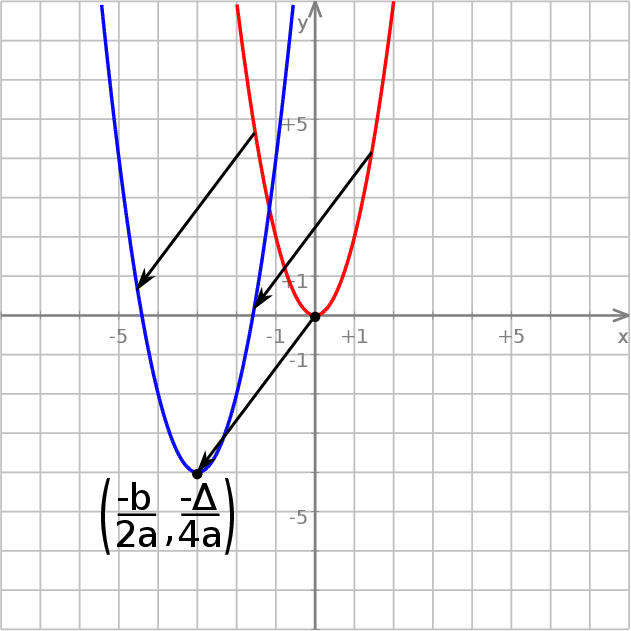
Ponadto wykres funkcji 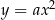 dla
dla 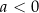 powstaje z wykresu funkcji
powstaje z wykresu funkcji 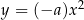 przez odbicie względem osi
przez odbicie względem osi 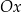 . Opisane własności wykresu funkcji
. Opisane własności wykresu funkcji 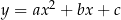 są więc natychmiastowymi konsekwencjami odpowiednich własności funkcji
są więc natychmiastowymi konsekwencjami odpowiednich własności funkcji 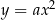 (Lemat 7).
(Lemat 7).
Nierówności kwadratowe
Twierdzenie 9
Rozwiązaniem nierówności 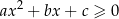 , gdzie
, gdzie 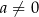 jest
jest
-
jeżeli
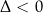 : zbiór pusty
: zbiór pusty 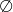 dla
dla 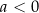 , oraz zbiór
, oraz zbiór 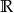 dla
dla 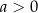 ;
; -
jeżeli
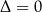 : zbiór jednoelementowy
: zbiór jednoelementowy 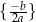 dla
dla 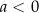 , oraz zbiór
, oraz zbiór 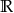 dla
dla 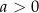 ;
; -
jeżeli
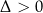 : przedział
: przedział 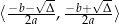 dla
dla 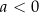 oraz zbiór
oraz zbiór 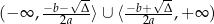 dla
dla 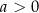 .
.
Dowód
-
Z Twierdzenia 8 wiemy, że zbiorem wartości funkcji
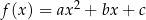 jest przedział
jest przedział 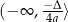 dla
dla 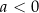 oraz przedział
oraz przedział 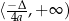 dla
dla 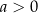 . Jeżeli
. Jeżeli 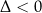 to zbiór ten jest w całości odpowiednio poniżej/powyżej osi
to zbiór ten jest w całości odpowiednio poniżej/powyżej osi 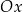 .
. -
Tak jak wyżej, ale tym razem mamy jeden punkt
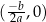 leżący na osi
leżący na osi 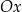 .
. -
Jeżeli
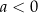 to z Twierdzenia 8 wiemy, że funkcja
to z Twierdzenia 8 wiemy, że funkcja 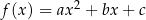 jest rosnąca na przedziale
jest rosnąca na przedziale 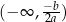 . Ponadto, na mocy Twierdzenia 2, wiemy, że ma ona w tym przedziale miejsce zerowe
. Ponadto, na mocy Twierdzenia 2, wiemy, że ma ona w tym przedziale miejsce zerowe 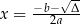 . Musi więc być ujemna na przedziale
. Musi więc być ujemna na przedziale 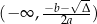 i dodatnia na przedziale
i dodatnia na przedziale 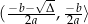 . Podobnie rozumujemy dla przedziału
. Podobnie rozumujemy dla przedziału 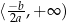 oraz dla
oraz dla 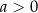 .
.
Symetrie paraboli
Twierdzenie 10
Parabola 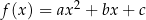 ma dokładnie jedną oś symetrii i jest nią prosta
ma dokładnie jedną oś symetrii i jest nią prosta 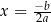 .
.
Dowód Wiemy już (Twierdzenie 8), że prosta 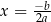 jest osią symetrii wykresu. Pozostało uzasadnić, że wykres nie ma innych osi symetrii.
jest osią symetrii wykresu. Pozostało uzasadnić, że wykres nie ma innych osi symetrii.
Wiemy, że każda parabola jest przesunięciem paraboli 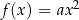 , więc wystarczy zająć się tym przypadkiem. W dodatku przypadek
, więc wystarczy zająć się tym przypadkiem. W dodatku przypadek 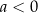 sprowadza się do przypadku
sprowadza się do przypadku 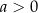 przez odbicie względem osi
przez odbicie względem osi 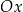 , więc możemy założyć, że
, więc możemy założyć, że 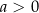 .
.
Załóżmy, że jest jeszcze jedna oś symetrii, powiedzmy 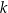 .
.
Jeżeli 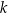 jest pionową prostą, to musi przeprowadzać punkt
jest pionową prostą, to musi przeprowadzać punkt 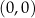 na punkt na wykresie o drugiej współrzędnej równej 0, a wiemy, że na wykresie jest tylko jeden taki punkt (Lemat 7), więc w takiej sytuacji
na punkt na wykresie o drugiej współrzędnej równej 0, a wiemy, że na wykresie jest tylko jeden taki punkt (Lemat 7), więc w takiej sytuacji 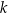 musi być prostą
musi być prostą 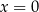 , co jest sprzeczne z naszym założeniem.
, co jest sprzeczne z naszym założeniem.
Możemy zatem założyć, że prosta 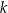 ma równanie
ma równanie 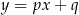 . Rozważmy funkcję
. Rozważmy funkcję 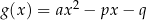 . Miejsca zerowe tej funkcji odpowiadają punktom wspólnym paraboli
. Miejsca zerowe tej funkcji odpowiadają punktom wspólnym paraboli 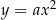 i prostej
i prostej 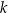 , wartości dodatnie tej funkcji odpowiadają punktom w których parabola
, wartości dodatnie tej funkcji odpowiadają punktom w których parabola 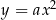 jest powyżej prostej
jest powyżej prostej 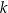 , a wartości ujemne punktom, w których parabola jest poniżej prostej
, a wartości ujemne punktom, w których parabola jest poniżej prostej 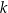 . Spróbujmy teraz rozważyć wszystkie możliwe konfiguracje (wiemy jakie są możliwości z Twierdzenia 9).
. Spróbujmy teraz rozważyć wszystkie możliwe konfiguracje (wiemy jakie są możliwości z Twierdzenia 9).
Jeżeli funkcja 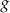 nie ma w ogóle, lub ma jedno miejsce zerowe, to cała parabola jest po jednej stronie prostej
nie ma w ogóle, lub ma jedno miejsce zerowe, to cała parabola jest po jednej stronie prostej 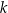 , więc prosta ta nie może być jej osią symetrii.
, więc prosta ta nie może być jej osią symetrii.
Jeżeli funkcja 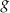 ma dwa miejsca zerowe, to po jednej stronie prostej
ma dwa miejsca zerowe, to po jednej stronie prostej 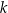 jest ograniczony łuk paraboli łączący te punkty przecięcia (odpowiada on rozwiązaniom nierówności
jest ograniczony łuk paraboli łączący te punkty przecięcia (odpowiada on rozwiązaniom nierówności 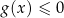 ), a po drugiej stronie jest zbiór nieograniczony (odpowiadający rozwiązaniom nierówności
), a po drugiej stronie jest zbiór nieograniczony (odpowiadający rozwiązaniom nierówności 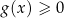 ).
).
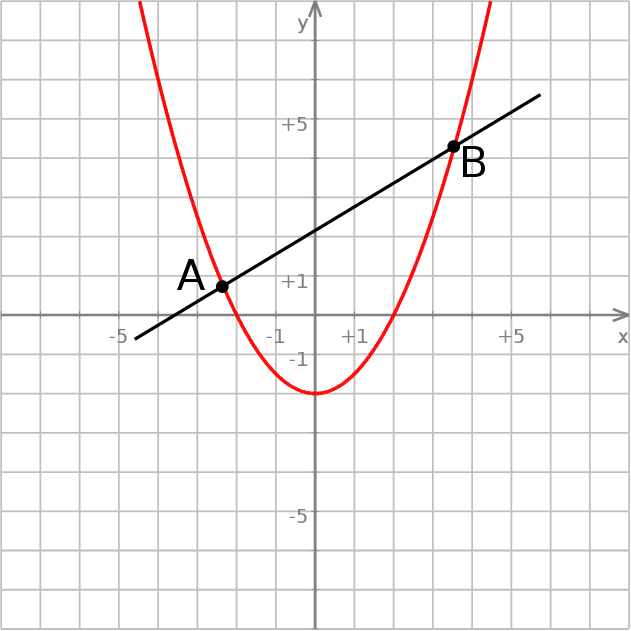
Tak więc i w tym przypadku prosta 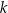 nie może być osią symetrii paraboli.
nie może być osią symetrii paraboli.
Podobieństwo parabol
Twierdzenie 11
Każde dwie parabole są podobne.
Dowód Tak jak w poprzednim twierdzeniu, zauważamy, że wystarczy zajmować się parabolami postaci 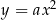 , gdzie
, gdzie 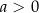 . Pokażemy, że każda parabola tej postaci jest obrazem w jednokładności o środku w punkcie
. Pokażemy, że każda parabola tej postaci jest obrazem w jednokładności o środku w punkcie 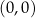 paraboli
paraboli 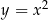 .
.
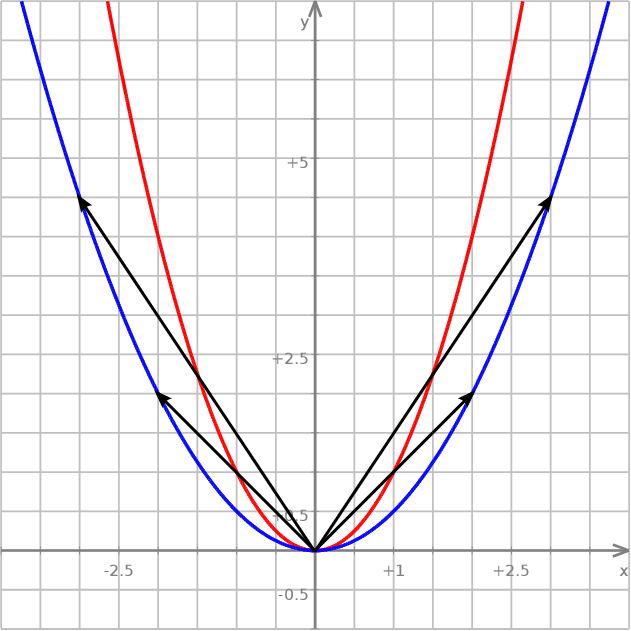
Rzeczywiście, niech 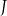 będzie taką jednokładnością o skali
będzie taką jednokładnością o skali  . Wtedy obrazem paraboli
. Wtedy obrazem paraboli 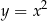 jest zbiór opisany równaniem
jest zbiór opisany równaniem
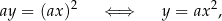
czyli parabola 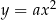 .
.
3 punkty na paraboli
Twierdzenie 12
Dla dowolnych trzech punktów 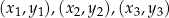 , gdzie
, gdzie
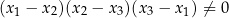
(tzn. liczby 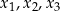 są parami różne), które nie leżą na jednej prostej, istnieje dokładnie jedna parabola
są parami różne), które nie leżą na jednej prostej, istnieje dokładnie jedna parabola 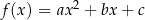 przechodząca przez te punkty.
przechodząca przez te punkty.
Dowód Mamy do rozwiązania układ równań
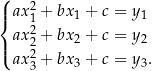
Odejmując od drugiego i od trzeciego równania pierwsze dostajemy układ
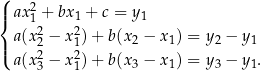
Zauważmy, że niewiadoma  występuje tylko w pierwszym równaniu i w dodatku równanie to pozwala jednoznacznie ją wyliczyć jeżeli znamy
występuje tylko w pierwszym równaniu i w dodatku równanie to pozwala jednoznacznie ją wyliczyć jeżeli znamy  i
i 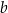 . W takim razie wystarczy zająć się dwoma pozostałymi równaniami, czyli układem
. W takim razie wystarczy zająć się dwoma pozostałymi równaniami, czyli układem
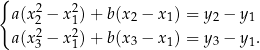
Stosujemy teraz metodę wyznacznikową.
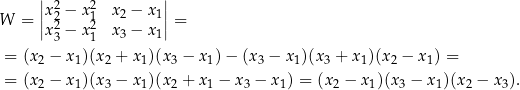
Liczba ta jest niezerowa z założenia, więc wiemy, że układ ten ma dokładnie jedno rozwiązanie. Ostatnia rzecz, którą musimy sprawdzić, to czy przypadkiem nie wyjdzie 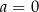 . Sprawdźmy kiedy tak jest
. Sprawdźmy kiedy tak jest
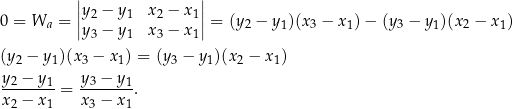
Ta równość oznacza jednak, że wektory ![[x2 − x ,y2 − y ] 1 1](https://img.zadania.info/por/0021995/HporT242x.png) i
i ![[y3 − y ,x3 − x ] 1 1](https://img.zadania.info/por/0021995/HporT243x.png) są równoległe (w powyżej równości mamy tangensy kątów jakie tworzą one z osią
są równoległe (w powyżej równości mamy tangensy kątów jakie tworzą one z osią 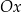 ). To jednak oznacza, że dane trzy punkty leżą na jednej prostej, co jest sprzeczne z naszym założeniem.
). To jednak oznacza, że dane trzy punkty leżą na jednej prostej, co jest sprzeczne z naszym założeniem.
Wniosek 13
Jeżeli dwie parabole 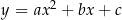 i
i 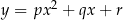 mają trzy punkty wspólne, to
mają trzy punkty wspólne, to 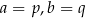 i
i 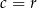 .
.
Dowód Szukanie punktów wspólnych paraboli i prostej prowadzi do rozwiązywania równania kwadratowego. Zatem parabola i prosta zawsze przecinają się w nie więcej niż 2 punktach. W takim razie punkty, o których mowa w treści twierdzenia, nie leżą na jednej prostej i możemy do nich zastosować Twierdzenie 12. Z twierdzenia tego wiemy, że istnieje dokładnie jedna parabola przechodząca przez te trzy punkty. Dane parabole muszą się więc pokrywać.
Wniosek 14
Dla dowolnych dwóch punktów 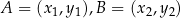 , gdzie
, gdzie 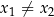 i
i 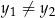 istnieje dokładnie jedna parabola
istnieje dokładnie jedna parabola 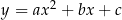 o wierzchołku w punkcie
o wierzchołku w punkcie 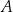 i przechodząca przez punkt
i przechodząca przez punkt 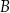
Dowód Niech 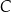 będzie obrazem punktu
będzie obrazem punktu 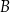 w symetrii względem pionowej prostej przechodzącej przez
w symetrii względem pionowej prostej przechodzącej przez 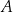 . Zauważmy, że przy naszych założeniach, punkty
. Zauważmy, że przy naszych założeniach, punkty 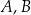 i
i 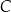 nie leżą na jednej prostej.
nie leżą na jednej prostej.
Na mocy Twierdzenia 8 wiemy, że każda parabola o wierzchołku w 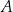 i przechodząca przez
i przechodząca przez 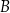 musi przechodzić przez punkt
musi przechodzić przez punkt 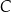 . To, na mocy Twierdzenia 12, daje nam istnienie i jednoznaczność: wiemy, że dla 3 ustalonych punktów parabola istnieje i jest dokładnie jedna.
. To, na mocy Twierdzenia 12, daje nam istnienie i jednoznaczność: wiemy, że dla 3 ustalonych punktów parabola istnieje i jest dokładnie jedna.
Jako natychmiastowy wniosek otrzymujemy.
Wniosek 15
Jeżeli dwie parabole 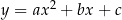 i
i 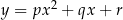 mają wspólny wierzchołek i jeszcze jeden dodatkowy punkt, to
mają wspólny wierzchołek i jeszcze jeden dodatkowy punkt, to 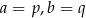 i
i 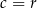 .
.
Tips & Tricks
1Nasza definicja paraboli jest typowo szkolna i jej główną wadą jest to, że w ten sposób definiujemy tylko pionowe parabole. Zgodnie z naszą definicją, obrócona parabola przestaje być parabolą. Tak naprawdę parabolę powinno się definiować jako zbiór punktów, które są równo odległe od ustalonego punktu (ogniska paraboli) i ustalonej prostej (kierownicy paraboli).
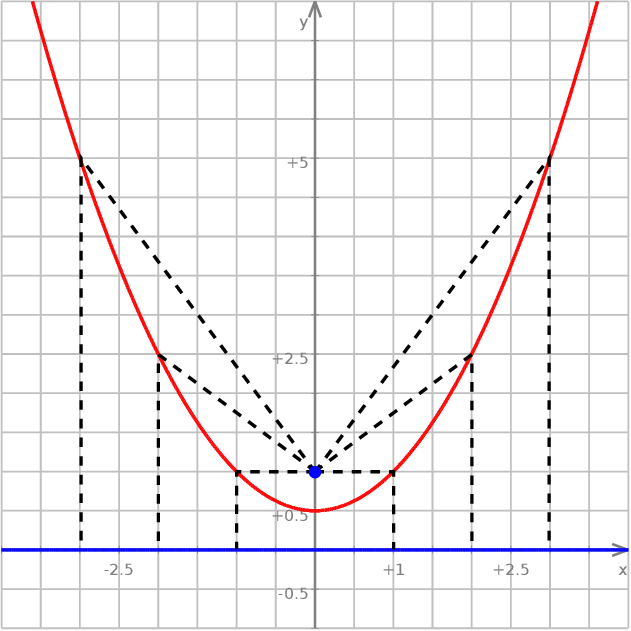
W przypadku poziomej kierownicy otrzymujemy pionowe parabole.
2Zupełnie naturalne jest pytanie o wzory na pierwiastki, podobne do tych z Twierdzenia 2, dla wielomianów wyższych stopni. Okazuje się, że wzory takie można wyprowadzić dla wielomianów stopni 3 i 4 (choć są bardzo skomplikowane). Można natomiast udowodnić, że wzory takie nie istnieją dla wielomianów stopnia co najmniej 5.
3Uogólnieniem Wniosku 3 na dowolne wielomiany jest twierdzenie Bézouta, z którego wynika, że wielomian stopnia  , który ma
, który ma  pierwiastków (licząc z krotnościami) rozkłada się na iloczyn czynników liniowych. Innym uogólnieniem jest znacznie trudniejszy w dowodzie fakt, że każdy wielomian można rozłożyć na iloczyn czynników liniowych i kwadratowych. Aby zobaczyć, że nie jest to oczywiste, polecam znaleźć taki rozkład dla
pierwiastków (licząc z krotnościami) rozkłada się na iloczyn czynników liniowych. Innym uogólnieniem jest znacznie trudniejszy w dowodzie fakt, że każdy wielomian można rozłożyć na iloczyn czynników liniowych i kwadratowych. Aby zobaczyć, że nie jest to oczywiste, polecam znaleźć taki rozkład dla 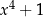 .
.
4Jeżeli komuś się wydaje, że Twierdzenie 4 jest oczywiste, to niech sobie pomyśli o funkcjach 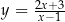 i
i 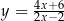 , albo o funkcjach
, albo o funkcjach 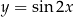 i
i 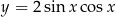 . Pomimo, że wzory tych funkcji wyglądają zupełnie inaczej, są to dokładnie te same funkcje. To co dowodzimy w Twierdzeniu 4, to że dla funkcji kwadratowych tego typu sytuacje (tożsamości) nie są możliwe.
. Pomimo, że wzory tych funkcji wyglądają zupełnie inaczej, są to dokładnie te same funkcje. To co dowodzimy w Twierdzeniu 4, to że dla funkcji kwadratowych tego typu sytuacje (tożsamości) nie są możliwe.
Co więcej, jeżeli zmienimy dziedzinę wielomianów, to twierdzenie to może nie być prawdziwe. Np. w informatyce często rozważa się funkcje, których dziedziną jest zbiór 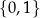 . W takiej sytuacji funkcje
. W takiej sytuacji funkcje 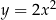 i
i 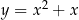 są identyczne.
są identyczne.
5W przypadku funkcji kwadratowej, wzory Viète’a można uzasadnić bezpośrednio ze wzorów na pierwiastki, wtedy nie jest potrzebne Twierdzenie 4. Jednak taki dowód nie przenosi się w żaden sposób na wielomiany wyższych stopni. Nasze uzasadnienie w zasadzie bez zmian funkcjonuje w przypadku wielomianów dowolnego stopnia. "W zasadzie", bo zarówno Twierdzenie 4 jak i istnienie postaci iloczynowej (tzw. twierdzenie Bézouta) są w tej sytuacji odrobinę trudniejsze w dowodzie.
6Twierdzenie 6 należy rozumieć jako twierdzenie odwrotne do wzorów Viète’a – jego sens jest taki, że wzory Viète’a są równoważne samemu równaniu kwadratowemu. Własność ta jest bardzo wygodna w wielu zadaniach. Np. mając układ równań 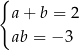 wiemy, że liczby
wiemy, że liczby  i
i 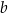 są pierwiastkami równania
są pierwiastkami równania 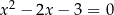 .
.
7Lemat 7 oraz Twierdzenie 8 stanowią uzasadnienie dobrze znanych własności paraboli. Żeby było jasne, takie uzasadnienie jest potrzebne i właśnie z niego wynika, że to co rysujemy myśląc o paraboli wygląda tak, jak się tego nauczyliśmy. Mówiąc jeszcze inaczej, właśnie dowody mówią o tym jak wygląda wykres funkcji, a nie np. robione na komputerze obrazki.
Weźmy na przykład funkcję 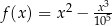 .
.
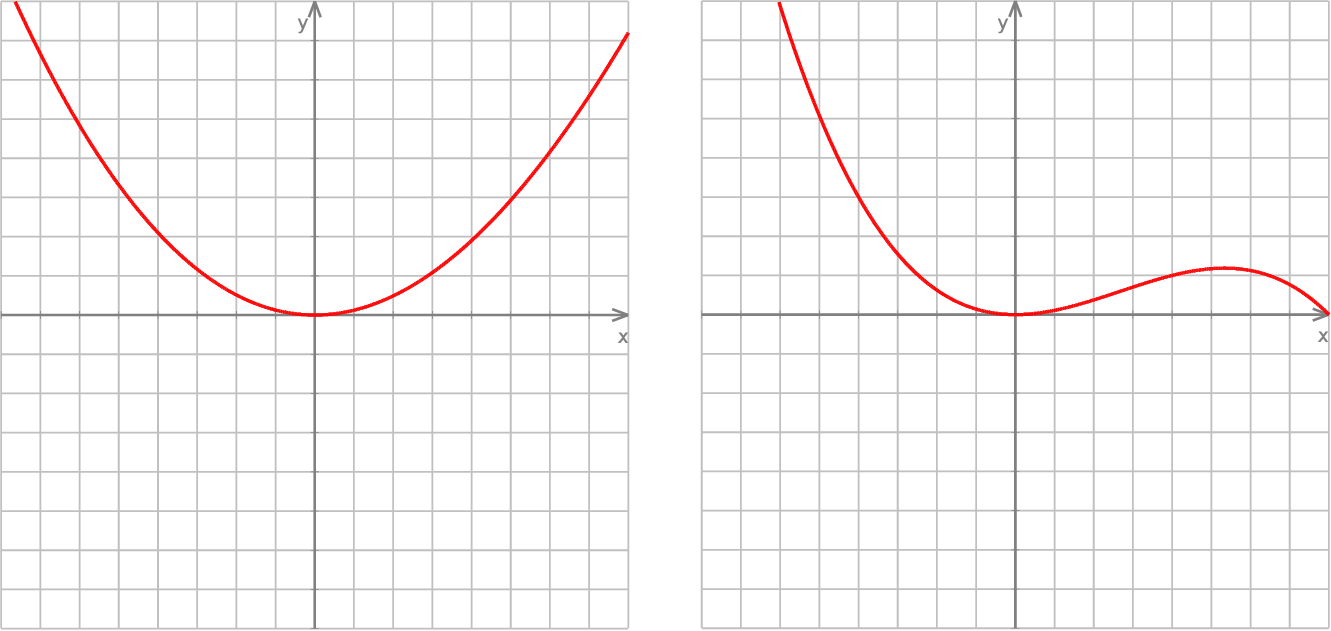
Uważam, że bardzo dobrym ćwiczeniem jest próba ustalenia jak wygląda wykres tej funkcji, używając jakiegoś programu do rysowania wykresów. Jeżeli będziemy brali "małe" wartości na osi 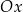 , to wykres będzie nieodróżnialny od paraboli – na lewym wykresie
, to wykres będzie nieodróżnialny od paraboli – na lewym wykresie  zmienia się w przedziale
zmienia się w przedziale 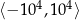 (oś
(oś 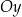 jest przeskalowana do
jest przeskalowana do 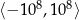 żeby wykres ładnie wyglądał). Dopiero gdy na osi
żeby wykres ładnie wyglądał). Dopiero gdy na osi 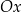 zbliżymy się do przedziału
zbliżymy się do przedziału 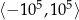 (prawy wykres) zaczyna być widać, że to jednak nie jest parabola.
(prawy wykres) zaczyna być widać, że to jednak nie jest parabola.
Może dla funkcji 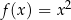 też tak jest? – nie, nie jest i to właśnie uzasadniamy w Lemacie 7/Twierdzeniu 8.
też tak jest? – nie, nie jest i to właśnie uzasadniamy w Lemacie 7/Twierdzeniu 8.
8Warunek wypukłości wygląda na bardzo skomplikowany, ale ma bardzo prostą interpretację geometryczną: oznacza on, że jeżeli weźmiemy dowolne dwa punkty 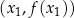 i
i 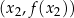 na wykresie funkcji
na wykresie funkcji 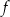 , odcinek łączący te punkty jest w całości powyżej wykresu funkcji
, odcinek łączący te punkty jest w całości powyżej wykresu funkcji 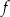 .
.
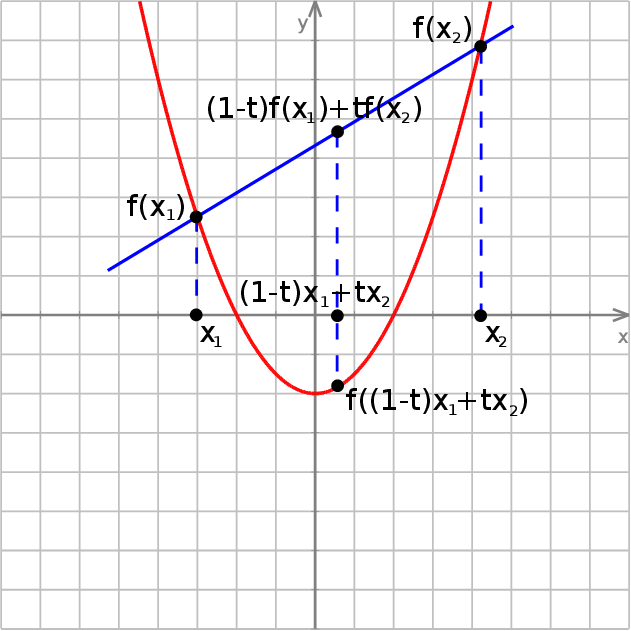
Zapis 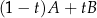 to standardowa parametryzacja odcinka o końcach
to standardowa parametryzacja odcinka o końcach 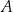 i
i 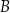 : dla
: dla 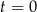 mamy
mamy 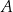 , dla
, dla 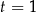 mamy
mamy 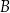 , dla
, dla 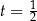 mamy środek odcinka itd.
mamy środek odcinka itd.
O wypukłości należy myśleć jak o kierunku, w którym wygina się wykres: jeżeli jedziemy zgodnie ze strzałką narysowaną na osi 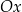 , to wykres funkcji wypukłej skręca w lewo. Wykres funkcji wklęsłej (np.
, to wykres funkcji wypukłej skręca w lewo. Wykres funkcji wklęsłej (np. 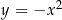 ) skręca w prawo. To, jak szybko ten wykres skręca, mierzy druga pochodna funkcji.
) skręca w prawo. To, jak szybko ten wykres skręca, mierzy druga pochodna funkcji.
9W twierdzeniu 9 zajęliśmy się tylko nierównością typu "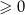 ", ale oczywiście łatwo z tego przypadku wywnioskować rozwiązania pozostałych możliwych nierówności: "
", ale oczywiście łatwo z tego przypadku wywnioskować rozwiązania pozostałych możliwych nierówności: "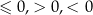 ".
".
10Twierdzenie 10 zasługuje na specjalny komentarz, bo jest notorycznie wykorzystywane w zadaniach szkolnych, chociaż nikt go jawnie nie wypowiada (i nie znajdziemy go w podręcznikach szkolnych). Każde zadanie typu wyznacz oś symetrii wykresu funkcji 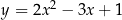 wymaga znajomości tego twierdzenia, tzn. musimy wiedzieć, że podawana w odpowiedzi prosta
wymaga znajomości tego twierdzenia, tzn. musimy wiedzieć, że podawana w odpowiedzi prosta 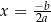 jest jedyną osią symetrii. Co więcej, jak popatrzymy na dowód tego twierdzenia, to nie jest on może bardzo trudny, ale nie jest też zupełnie prosty (i niektóre rzeczy, np. "ograniczoność łuku" pozostawiliśmy w nim na mało precyzyjnym poziomie). W takiej sytuacji rodzi się pytanie o sensowność tego typu zadań w podręcznikach szkolnych. Fakt, że takie zadania są w podręcznikach zupełnie powszechne, niestety jest często przejawem ignorancji ich autorów.
jest jedyną osią symetrii. Co więcej, jak popatrzymy na dowód tego twierdzenia, to nie jest on może bardzo trudny, ale nie jest też zupełnie prosty (i niektóre rzeczy, np. "ograniczoność łuku" pozostawiliśmy w nim na mało precyzyjnym poziomie). W takiej sytuacji rodzi się pytanie o sensowność tego typu zadań w podręcznikach szkolnych. Fakt, że takie zadania są w podręcznikach zupełnie powszechne, niestety jest często przejawem ignorancji ich autorów.
Inny problem jest z zadaniami typu: prosta 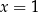 jest osią symetrii wykresu funkcji
jest osią symetrii wykresu funkcji 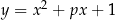 , wyznacz
, wyznacz 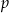 . To zadanie można rozwiązać nie używając Twierdzenia 10: bierzemy jakiś punkt z wykresu, np.
. To zadanie można rozwiązać nie używając Twierdzenia 10: bierzemy jakiś punkt z wykresu, np. 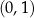 , potem sprawdzamy kiedy obraz tego punktu w symetrii względem
, potem sprawdzamy kiedy obraz tego punktu w symetrii względem 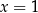 (czyli punkt
(czyli punkt 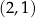 ) też jest na wykresie, daje nam to
) też jest na wykresie, daje nam to 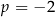 . Pytanie natomiast brzmi, czy rozwiązanie w stylu: osią symetrii wykresu tej funkcji jest prosta
. Pytanie natomiast brzmi, czy rozwiązanie w stylu: osią symetrii wykresu tej funkcji jest prosta 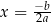 , więc mamy równanie
, więc mamy równanie 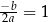 itd., uznać za poprawne. W takim rozwiązaniu korzystamy już z Twierdzenia 11 i moim zdaniem, jeżeli mamy przesłanki, że autor rozwiązania nie jest tego świadomy (a tak jest w zasadzie zawsze), to takie rozwiązanie należy uznać za błędne.
itd., uznać za poprawne. W takim rozwiązaniu korzystamy już z Twierdzenia 11 i moim zdaniem, jeżeli mamy przesłanki, że autor rozwiązania nie jest tego świadomy (a tak jest w zasadzie zawsze), to takie rozwiązanie należy uznać za błędne.
11To, że każdą parabolę 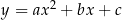 można przesunąć do paraboli
można przesunąć do paraboli 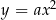 jest w sumie dość niezwykłe, bo pokazuje, że kształt paraboli (z dokładnością do przesunięcia) zależy tylko od jednego parametru (pomimo, że sam wzór funkcji zależy od 3). Twierdzenie 11 jest jeszcze bardziej zaskakujące, bo pokazuje, że jeżeli dopuścimy zmianę skali, to parabola jest tylko jedna.
jest w sumie dość niezwykłe, bo pokazuje, że kształt paraboli (z dokładnością do przesunięcia) zależy tylko od jednego parametru (pomimo, że sam wzór funkcji zależy od 3). Twierdzenie 11 jest jeszcze bardziej zaskakujące, bo pokazuje, że jeżeli dopuścimy zmianę skali, to parabola jest tylko jedna.
12Twierdzenie 12 nie jest specjalnie zaskakujące: we wzorze 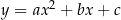 mamy trzy parametry, więc nic dziwnego, że potrzebujemy trzech warunków, żeby je jednoznacznie wyliczyć. Dowód tego twierdzenia byłby trochę prostszy, gdybyśmy skorzystali z metody wyznacznikowej rozwiązywania układu trzech równań z trzema niewiadomymi.
mamy trzy parametry, więc nic dziwnego, że potrzebujemy trzech warunków, żeby je jednoznacznie wyliczyć. Dowód tego twierdzenia byłby trochę prostszy, gdybyśmy skorzystali z metody wyznacznikowej rozwiązywania układu trzech równań z trzema niewiadomymi.
13Twierdzenie 12 w naturalny sposób uogólnia się na wielomiany dowolnego stopnia: dla dowolnych 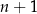 punktów
punktów 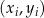 , gdzie
, gdzie 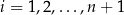 oraz
oraz 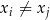 dla
dla 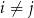 , istnieje wielomian stopnia co najwyżej
, istnieje wielomian stopnia co najwyżej  , którego wykres przechodzi przez te punkty. Gdybyśmy chcieli mieć w tezie dokładnie wielomian stopnia
, którego wykres przechodzi przez te punkty. Gdybyśmy chcieli mieć w tezie dokładnie wielomian stopnia  , to musimy dodatkowo założyć, że punkty te nie leżą na wykresie wielomianu stopnia
, to musimy dodatkowo założyć, że punkty te nie leżą na wykresie wielomianu stopnia 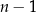 .
.
Podobnie uogólnia się Wniosek 13: jeżeli wykresy dwóch wielomianów stopnia  mają
mają 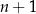 punktów wspólnych to się pokrywają.
punktów wspólnych to się pokrywają.
14Wiemy, że 3 punkty jednoznacznie wyznaczają parabolę. Jaki jest jej wzór? Przy odrobinie sprytu można go wymyślić:
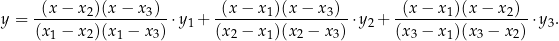
Żeby zobaczyć, że jest dobrze, wystarczy podstawić w tym wzorze kolejno 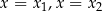 i
i 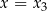 .
.
Jako ćwiczenie polecam napisanie analogicznego wzoru dla wielomianu stopnia 3 (trzeba wziąć 4 punkty).
15Wniosek 13 jest oczywiście dużym wzmocnieniem Twierdzenia 4, ale ponieważ dowód Twierdzenia 4 jest o wiele prostszy, postanowiliśmy potraktować te fakty niezależnie.
16Wniosek 14 jest ciekawy, bo pokazuje, że wierzchołek jest bardzo szczególnym punktem paraboli – jego ustalenie zostawia bardzo mało swobody na możliwe kształty paraboli. Oczywiście powodem jest symetria paraboli względem pionowej prostej przechodzącej przez wierzchołek: wybór wierzchołka ustala oś symetrii paraboli.

