Jak wyglądają równania i nierówności wszyscy mniej więcej wiemy, więc nie będziemy się tu bawić w definicje. Zamiast tego przypomnijmy, że rozwiązanie równania/nierówności powinno zawsze składać się z dwóch etapów:
-
Przekształcenie równania/nierówności do prostszej postaci, z której da się łatwo odczytać wszystkie możliwe rozwiązania.
-
Sprawdzenie, które z rozwiązań przekształconego równania/nierówności są też rozwiązaniami równania/nierówności, które mieliśmy rozwiązać.
W pierwszej chwili powyższe dwa punkty mogą budzić zdziwienie (pewnie nigdy nie rozwiązywaliście równania w dwóch krokach), ale warto zdobyć się na wysiłek i zrozumieć tę uwagę, bo pozwala ona uniknąć wielu błędów i nieporozumień przy rozwiązywaniu zadań. Jeżeli liczby są równe, to są równe Przekształcanie równań opiera się na banalnym stwierdzeniu zawartym w tytule tego akapitu. Powiedzmy, że chcemy rozwiązać równanie 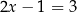 . Robimy to tak: skoro
. Robimy to tak: skoro 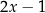 jest równe
jest równe 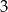 , to jeżeli wykonamy jakąkolwiek operację algebraiczną na obu tych liczbach na raz, to nadal będą równe. Z tego właśnie powodu możemy do tej równości dodać, co tylko chcemy, możemy ją pomnożyć przez co tylko chcemy, możemy ją podnieść do kwadratu, możemy zlogarytmować (jeżeli są dodatnie) itd. Skoro wystartowaliśmy od liczb, które są równe, po każdej takiej operacji będziemy mieć liczby równe. I to jest dokładnie przekształcanie równań.
, to jeżeli wykonamy jakąkolwiek operację algebraiczną na obu tych liczbach na raz, to nadal będą równe. Z tego właśnie powodu możemy do tej równości dodać, co tylko chcemy, możemy ją pomnożyć przez co tylko chcemy, możemy ją podnieść do kwadratu, możemy zlogarytmować (jeżeli są dodatnie) itd. Skoro wystartowaliśmy od liczb, które są równe, po każdej takiej operacji będziemy mieć liczby równe. I to jest dokładnie przekształcanie równań.
Przekształćmy równanie 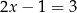 tak, aby było widać jakie jest jego rozwiązanie.
tak, aby było widać jakie jest jego rozwiązanie.
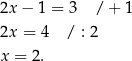
Zwróćmy uwagę, że w pierwszym kroku dodaliśmy do obu stron 1 – na ogół mówi się krótko, że przenieśliśmy -1 na prawą stronę. Tak więc przenoszenie z jednej strony równania na drugą to nic innego, jak dodawanie do obu stron równania tej samej liczby.
Zadajmy sobie teraz niezwykle ważne pytanie: skąd wiemy, że wyliczona w powyższym przykładzie wartość 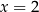 rzeczywiście spełnia równanie, które mieliśmy rozwiązać? Głupie pytanie? Niekoniecznie, co łatwo zobaczyć na przykładach.
rzeczywiście spełnia równanie, które mieliśmy rozwiązać? Głupie pytanie? Niekoniecznie, co łatwo zobaczyć na przykładach.
Przekształćmy równanie 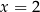 podnosząc je stronami do kwadratu. Mamy więc
podnosząc je stronami do kwadratu. Mamy więc
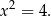
Zatem 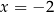 lub
lub 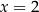 . Oczywiście tylko druga z tych liczb jest rozwiązaniem równania, od którego wystartowaliśmy.
. Oczywiście tylko druga z tych liczb jest rozwiązaniem równania, od którego wystartowaliśmy.
Wyjściową równość mogliśmy przekształcić jeszcze brutalniej, możemy obie strony pomnożyć przez 0 i otrzymamy równanie 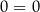 , które jest spełnione przez każdą liczbę.
, które jest spełnione przez każdą liczbę.
Rozwiążmy równanie 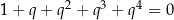 .
.
Ze wzoru na sumę początkowych wyrazów ciągu geometrycznego mamy
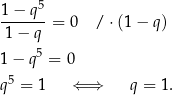
Łatwo sprawdzić, że 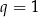 wcale nie jest rozwiązaniem wyjściowego równania.
wcale nie jest rozwiązaniem wyjściowego równania.
Rozwiążmy równanie 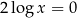 .
.
Na mocy dobrze znanego wzoru 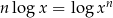 , możemy to równanie zapisać w postaci
, możemy to równanie zapisać w postaci
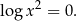
Zatem 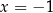 lub
lub 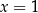 . Jednak tylko druga z tych liczb spełnia wyjściowe równanie.
. Jednak tylko druga z tych liczb spełnia wyjściowe równanie.
Po tych przykładach radzę jeszcze raz przeczytać pierwszy akapit tego poradnika. Powinno być teraz jasne, że przekształcenie równania do prostszej postaci to tylko połowa pracy. Równoważność, a implikacja Jednak w przypadku pierwszego przykładu: 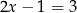 raczej nie mamy wątpliwości, że otrzymane rozwiązanie
raczej nie mamy wątpliwości, że otrzymane rozwiązanie 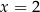 jest poprawne. Dlaczego tak jest? Ano dlatego, że otrzymaliśmy je przekształcając równanie przy pomocy równoważności. Żeby dobrze zrozumieć o co chodzi, zapiszmy to przekształcenie używając znaczka implikacji
jest poprawne. Dlaczego tak jest? Ano dlatego, że otrzymaliśmy je przekształcając równanie przy pomocy równoważności. Żeby dobrze zrozumieć o co chodzi, zapiszmy to przekształcenie używając znaczka implikacji
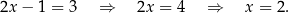
To co jest ważne, to że każdą z tych strzałek można odwrócić. Żeby nie było wątpliwości zapiszmy przekształcenia odpowiadające odwróceniu strzałek.
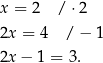
Powyższy rachunek jest sprawdzeniem, że rzeczywiście 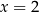 spełnia wyjściowe równanie. Aby podkreślić, że przekształcamy równanie przy pomocy równoważności, zwykle zapisujemy między kolejnymi krokami znak równoważności
spełnia wyjściowe równanie. Aby podkreślić, że przekształcamy równanie przy pomocy równoważności, zwykle zapisujemy między kolejnymi krokami znak równoważności
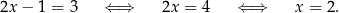
Dla porównania, zapiszmy przekształcenia z drugiego z przykładów.
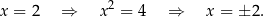
Mamy tu dwie implikacje, ale tylko druga z nich jest równoważnością. Implikacji
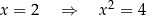
nie można odwrócić, tzn. nie jest prawdą, że z warunku 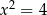 wynika, że
wynika, że 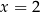 (bo może być też
(bo może być też 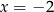 ). Dokładnie z tego powodu otrzymaliśmy fałszywe rozwiązanie
). Dokładnie z tego powodu otrzymaliśmy fałszywe rozwiązanie 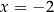 . Nierówności Na razie mówiliśmy tylko o równaniach, ale w przypadku nierówności sprawa jest jeszcze poważniejsza. Powód jest taki, że w przypadku równań zwykle rozwiązanie składa się tylko z kilku wartości, i nawet jak nie jesteśmy pewni czy wszystkie strzałki w naszych przekształceniach można odwrócić, to ostatecznie zawsze możemy posprawdzać otrzymane rozwiązania (podstawiając je do wyjściowego równania).
. Nierówności Na razie mówiliśmy tylko o równaniach, ale w przypadku nierówności sprawa jest jeszcze poważniejsza. Powód jest taki, że w przypadku równań zwykle rozwiązanie składa się tylko z kilku wartości, i nawet jak nie jesteśmy pewni czy wszystkie strzałki w naszych przekształceniach można odwrócić, to ostatecznie zawsze możemy posprawdzać otrzymane rozwiązania (podstawiając je do wyjściowego równania).
W przypadku nierówności sprawa się komplikuje, bo na ogół rozwiązaniem jest zbiór, który ma nieskończenie wiele elementów, więc sprawdzanie metodą podstawiania nie wchodzi w rachubę.
Rozwiążmy nierówność 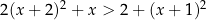 .
.
Liczymy
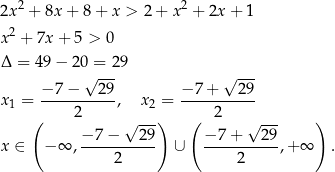
Jakie mamy teraz szanse na sprawdzenie, że liczby z otrzymanego zbioru rzeczywiście spełniają wyjściową nierówność? Szczerze mówiąc marne. W takiej sytuacji nie mamy wyjścia, musimy być pewni, że przekształcenia były równoważnościami.
Co wolno, a czego nie wolno Mając na uwadze powyższe przykłady powinno być jasne, że bardzo ważna jest umiejętność odróżniania przekształceń, które są równoważnościami od przekształceń, które są tylko implikacjami. Zacznijmy od przekształceń, które zawsze są równoważnościami:
-
proste operacje algebraiczne na jakichkolwiek składnikach równania, w szczególności dodawanie, mnożenie, odejmowanie, dzielenie, potęgowanie, pierwiastkowanie, stosowanie wzorów skróconego mnożenia, wymnażanie nawiasów, stosowanie tożsamości trygonometrycznych (jeżeli uważamy na zera mianowników);
-
dodanie do obu stron równania dowolnej liczby;
-
pomnożenie obu stron równania przez dowolną liczbę niezerową;
-
podniesienie obu stron równania do nieparzystej potęgi.
Do przekształceń, które na ogół nie są równoważnościami należą
-
podnoszenie równania stronami do parzystej potęgi;
-
obustronne mnożenie równania przez 0;
-
stosowanie wzorów z logarytmami (jeżeli jest w tych wzorach niewiadoma);
-
przykładanie do obu stron równości wartości bezwzględnej;
Jak to zapamiętać? Oczywiście najlepszy sposób to trening, ale ogólna rada jest następująca: wykonując jakiekolwiek przekształcenia równania, czy nierówności, cały czas miejmy z tyłu głowy pytanie, czy zastosowane przekształcenie można odwrócić. Powinno być jasne, że przy prostych przekształceniach zawsze da się to zrobić, ale gdy podnosimy równanie/nierówność do kwadratu, to powinna nam się zapalić czerwona żaróweczka. Jak z implikacji zrobić równoważność Mieliśmy przed chwilą ’czarną listę’ złych przekształceń, czy to oznacza, że nie możemy ich używać? Oczywiście możemy, a bardzo często wręcz musimy. W wielu przykładach jest to jedyny sposób na rozwiązanie równania, czy też nierówności.
Problem implikacji w przekształceniach można rozwiązać na dwa sposoby.
1. Można pogodzić się z tym, że przekształcamy równanie/nierówność tylko przy pomocy implikacji, a na koniec sprawdzić otrzymane rozwiązania. Metoda ta jest bardzo wygodna w przypadku równań (szczególnie logarytmicznych) – przekształcamy beztrosko równanie, a na koniec sprawdzamy otrzymane rozwiązania.
Rozwiążmy równanie 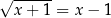 .
.
Musimy pozbyć się pierwiastka, więc podnosimy równanie stronami do kwadratu.
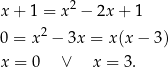
Łatwo sprawdzić, że tylko 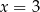 jest rozwiązaniem wyjściowego równania.
jest rozwiązaniem wyjściowego równania.
Rozwiążmy równanie 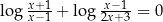 .
.
Gdybyśmy chcieli rozwiązać to równanie przy pomocy równoważności, to musielibyśmy wyznaczyć jego dziedzinę, a to jest bardzo nieprzyjemne zadanie (musimy sprawdzić kiedy obydwa wyrażenia pod logarytmami są dodatnie). Zamiast tego rozwiązujemy beztrosko, a na koniec sprawdzimy otrzymane rozwiązania.
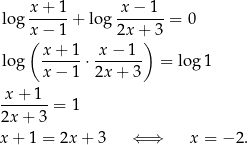
No i sprawdzamy
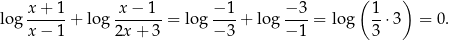
2. Powyższy sposób bywa bardzo elegancki, ale jak już pokazaliśmy w jednym z wcześniejszych przykładów, potrafi być całkowicie nieskuteczny w przypadku nierówności. Jedyne wyjście z takiej sytuacji to nałożenie na poszukiwaną niewiadomą dodatkowych założeń tak, aby ’zakazane przekształcenia’ zamieniły się w równoważności. W kolejnych podrozdziałach omówimy różne możliwe sytuacje.
Dziedzina Jeżeli chcemy przekształcać równanie/nierówność przy pomocy równoważności (tak aby nie sprawdzać otrzymanych rozwiązań), musimy rozpocząć od ustalenia jaka jest jego dziedzina. Jest to niezwykle ważny krok, co ilustrują poniższe przykłady.
Rozwiążmy równanie 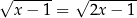
Obie strony są dodatnie, więc możemy podnieść obie strony do kwadratu (i jest to równoważność!).

Otrzymane rozwiązanie nie jest rozwiązaniem wyjściowego równania (pomimo, że przekształcaliśmy przy pomocy równoważności). Powód: nie sprawdziliśmy dziedziny równania.
Rozwiążmy równanie 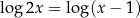 .
.
Logarytm jest różnowartościowy, więc możemy puścić logarytmy.
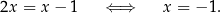
Otrzymane rozwiązanie jest błędne (chociaż przekształcenia są równoważnościami). Powód? Nie sprawdziliśmy dziedziny równania.
Podnoszenie do kwadratu Zacznijmy od podnoszenia równia stronami do parzystej potęgi (w szczególności do kwadratu). Aby tego typu przekształcenie było równoważnością, musimy wiedzieć, że obie strony mają ten sam znak (żeby z równości 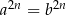 można było wywnioskować, że
można było wywnioskować, że 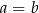 ). Ponieważ zawsze można zmienić znak obu stron równania/nierówności (mnożąc stronami przez -1), wystarczy zapamiętać, że podnoszenie do parzystej potęgi jest równoważnością jeżeli obie strony są nieujemne.
). Ponieważ zawsze można zmienić znak obu stron równania/nierówności (mnożąc stronami przez -1), wystarczy zapamiętać, że podnoszenie do parzystej potęgi jest równoważnością jeżeli obie strony są nieujemne.
Rozwiążmy raz jeszcze równanie 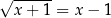 , ale tym razem postarajmy się je przekształcać w sposób równoważny. Zaczynamy od dziedziny:
, ale tym razem postarajmy się je przekształcać w sposób równoważny. Zaczynamy od dziedziny: 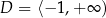 . Chcemy podnieść obie strony do kwadratu. Aby tego typu przekształcenie było równoważnością, musimy wiedzieć, że obie strony są nieujemne. Lewa jest zawsze nieujemna, więc nie ma problemu. Jeżeli prawa strona jest ujemna, czyli dla
. Chcemy podnieść obie strony do kwadratu. Aby tego typu przekształcenie było równoważnością, musimy wiedzieć, że obie strony są nieujemne. Lewa jest zawsze nieujemna, więc nie ma problemu. Jeżeli prawa strona jest ujemna, czyli dla 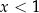 , to równanie jest na pewno sprzeczne (bo lewa strona jest nieujemna). Możemy więc założyć, że
, to równanie jest na pewno sprzeczne (bo lewa strona jest nieujemna). Możemy więc założyć, że 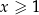 i przy tym założeniu możemy śmiało podnieść równanie stronami do kwadratu.
i przy tym założeniu możemy śmiało podnieść równanie stronami do kwadratu.
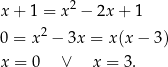
Pierwsze rozwiązanie nie spełnia naszego założenia 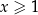 , zatem jedyne rozwiązanie to
, zatem jedyne rozwiązanie to 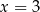 . Koniecznie trzeba tu podkreślić, że nie ma potrzeby sprawdzania, czy
. Koniecznie trzeba tu podkreślić, że nie ma potrzeby sprawdzania, czy 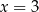 jest rozwiązaniem wyjściowego równania. Po to po drodze martwiliśmy się o równoważność, żeby tego uniknąć.
jest rozwiązaniem wyjściowego równania. Po to po drodze martwiliśmy się o równoważność, żeby tego uniknąć.
Rozwiążmy nierówność 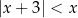 .
.
Dziedzina to 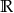 , więc nie ma tu problemu. Prosty sposób pozbycia się wartości bezwzględnej, to podniesienie nierówności stronami do kwadratu (bo
, więc nie ma tu problemu. Prosty sposób pozbycia się wartości bezwzględnej, to podniesienie nierówności stronami do kwadratu (bo 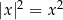 ). W tym celu zakładamy, że
). W tym celu zakładamy, że 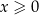 (dla
(dla 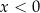 nierówność jest sprzeczna).
nierówność jest sprzeczna).
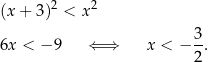
W połączeniu z naszym założeniem 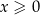 oznacza to, że nierówność jest sprzeczna.
oznacza to, że nierówność jest sprzeczna.
Tym razem rozwiążmy nierówność 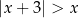 .
.
Nierówność wygląda bardzo podobnie jak nierówność w poprzednim przykładzie, ale jest odrobinę bardziej podchwytliwa. Ponownie chcemy podnieść ją stronami do kwadratu. Teraz jednak założenie 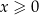 wcale nie jest automatyczne i musimy się temu dokładnie przyjrzeć. Jeżeli
wcale nie jest automatyczne i musimy się temu dokładnie przyjrzeć. Jeżeli 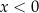 to prawa strona jest ujemna, a lewa niedodatnia, zatem nierówność jest spełniona. Pozostało rozpatrzyć przypadek
to prawa strona jest ujemna, a lewa niedodatnia, zatem nierówność jest spełniona. Pozostało rozpatrzyć przypadek 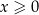 , a to robimy jak poprzednio.
, a to robimy jak poprzednio.
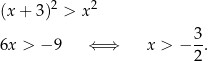
W połączeniu z założeniem 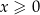 daje to zbiór
daje to zbiór 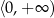 . Do tego zbioru musimy dodać jeszcze wcześniej otrzymany zbiór
. Do tego zbioru musimy dodać jeszcze wcześniej otrzymany zbiór 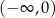 i widzimy, że nierówność jest spełniona przez każdą liczbę rzeczywistą.
i widzimy, że nierówność jest spełniona przez każdą liczbę rzeczywistą.
Mnożenie stronami przez 0 Może nie brzmi to poważnie, bo po co niby mnożyć stronami przez zero? No więc czasami robimy to niechcący, gdy mnożymy przez wyrażenie zawierające niewiadomą
Rozwiążmy równanie 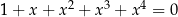 .
.
Równanie wygląda na trudne, ale jesteśmy sprytni i chcemy skorzystać ze wzoru
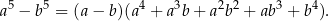
Mnożymy je więc stronami przez 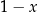 i mamy
i mamy
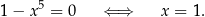
Otrzymane rozwiązanie jest niepoprawne. Powód? Dla 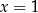 mnożyliśmy równanie stronami przez 0.
mnożyliśmy równanie stronami przez 0.
Co zrobić, żeby to rozwiązanie było poprawne? Jak zwykle mamy dwa wyjścia: albo sprawdzamy otrzymane rozwiązanie, albo jesteśmy ostrożniejsi przy mnożeniu stronami i zakładamy wtedy, że 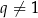 (a przypadek
(a przypadek 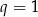 sprawdzamy osobno). Tak czy inaczej otrzymujemy poprawne uzasadnienie, że równanie jest sprzeczne.
sprawdzamy osobno). Tak czy inaczej otrzymujemy poprawne uzasadnienie, że równanie jest sprzeczne.
Powyższy przykład jest dość nietypowy, o wiele powszechniejszą sytuacją jest mnożenie przez mianowniki. W takim przypadku problem sam się rozwiązuje jeżeli tylko wyznaczymy dziedzinę równania/nierówności.
Rozwiążmy równanie 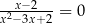 .
.
Mnożymy równanie stronami przez 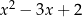 i mamy rozwiązanie
i mamy rozwiązanie 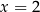 . Czy jest to dobre rozwiązanie? Jak zwykle mamy dwa wyjścia: albo sprawdzamy podstawiając, albo wyznaczamy dziedzinę równania i okaże się, że mnożyliśmy stronami przez 0 (dla
. Czy jest to dobre rozwiązanie? Jak zwykle mamy dwa wyjścia: albo sprawdzamy podstawiając, albo wyznaczamy dziedzinę równania i okaże się, że mnożyliśmy stronami przez 0 (dla 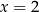 ). Oba sposoby dają nam poprawne uzasadnienie, że równanie jest sprzeczne.
). Oba sposoby dają nam poprawne uzasadnienie, że równanie jest sprzeczne.
Rozwiążmy równanie 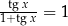 .
.
Liczymy
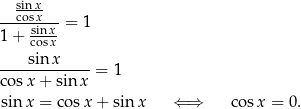
I teraz zagadka, skąd nam się wzięło fałszywe rozwiązanie? Z mnożenia przez 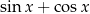 ? Nie, to wyrażenie jest niezerowe dla
? Nie, to wyrażenie jest niezerowe dla 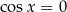 . Fałszywe rozwiązanie stworzyliśmy upraszczając
. Fałszywe rozwiązanie stworzyliśmy upraszczając 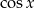 w piętrowych ułamkach. Właśnie wtedy zmieniliśmy dziedzinę równania mnożąc licznik i mianownik dużego ułamka przez 0 (dla
w piętrowych ułamkach. Właśnie wtedy zmieniliśmy dziedzinę równania mnożąc licznik i mianownik dużego ułamka przez 0 (dla 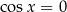 ). Jak zwykle, naprawić to możemy na dwa sposoby, ale akurat tutaj o wiele prościej jest sprawdzić otrzymane rozwiązanie niż sprawdzać kiedy
). Jak zwykle, naprawić to możemy na dwa sposoby, ale akurat tutaj o wiele prościej jest sprawdzić otrzymane rozwiązanie niż sprawdzać kiedy 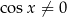 i
i 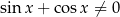 .
.
Rozwiążmy jeszcze nierówność 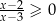 .
.
Mamy nierówność, więc chcemy zrobić to porządnie, żeby mieć pewność poprawności otrzymanych rozwiązań. Dziedzina to 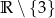 . Przy tym założeniu możemy śmiało mnożyć przez mianownik (jest niezerowy). Ponieważ jednak nie wiemy jaki ma znak, to mnożymy przez jego kwadrat, który z pewnością jest dodatni. Dostajemy zwykłą nierówność kwadratową.
. Przy tym założeniu możemy śmiało mnożyć przez mianownik (jest niezerowy). Ponieważ jednak nie wiemy jaki ma znak, to mnożymy przez jego kwadrat, który z pewnością jest dodatni. Dostajemy zwykłą nierówność kwadratową.
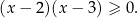
Jej rozwiązaniem jest zbiór 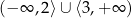 . Musimy jeszcze z tego zbioru wyrzucić
. Musimy jeszcze z tego zbioru wyrzucić 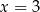 , bo nie należy do dziedziny.
, bo nie należy do dziedziny.
Wzory z logarytmami W przypadku stosowania wzorów z logarytmami sytuacja jest najbardziej podchwytliwa. W zasadzie każdy, nawet najprostszy wzór zmienia dziedzinę równania/nierówności, więc trzeba bardzo ostrożnie je stosować.
Rozwiążmy nierówność 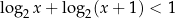 .
.
Liczymy
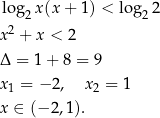
Tymczasem patrząc na nierówność widać gołym okiem, że  nie może być ujemny (bo jest pod logarytmem). W tym przykładzie problem można łatwo rozwiązać licząc na początku dziedzinę nierówności.
nie może być ujemny (bo jest pod logarytmem). W tym przykładzie problem można łatwo rozwiązać licząc na początku dziedzinę nierówności.
Co gorsza, możliwe jest tu całkowicie nowe zjawisko, mianowicie beztroskie przekształcanie może nie tylko dodawać fałszywe rozwiązania, ale może też gubić prawidłowe!
Rozwiążmy równanie 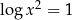 .
.
Korzystając ze wzoru 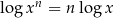 mamy
mamy
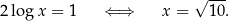
No i? No i zgubiliśmy rozwiązanie  . Stało się tak, bo stosując wzór
. Stało się tak, bo stosując wzór 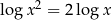 znacznie zmniejszyliśmy dziedzinę równania. Zauważmy, że tu nic nie pomoże wyliczenie dziedziny równania na początku. Mamy w tej konkretnej sytuacji dwa wyjścia: albo musimy ostrożniej stosować wzór
znacznie zmniejszyliśmy dziedzinę równania. Zauważmy, że tu nic nie pomoże wyliczenie dziedziny równania na początku. Mamy w tej konkretnej sytuacji dwa wyjścia: albo musimy ostrożniej stosować wzór 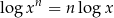 , albo możemy się nauczyć wzoru
, albo możemy się nauczyć wzoru 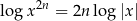 , który jest prawdziwy o ile tylko
, który jest prawdziwy o ile tylko 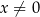 .
.
Rozwiążmy równanie 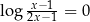 .
.
Korzystając ze wzoru na logarytm ilorazu mamy
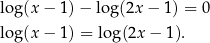
To równanie jest sprzeczne, bo po opuszczeniu logarytmów dostaniemy 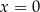 , które nie należy do dziedziny tego równania. Z drugiej strony,
, które nie należy do dziedziny tego równania. Z drugiej strony, 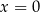 jest rozwiązaniem wyjściowego równania, więc zgubiliśmy je po drodze. Wyjścia są dwa: albo musimy być ostrożniejsi, albo musimy się nauczyć wzoru,
jest rozwiązaniem wyjściowego równania, więc zgubiliśmy je po drodze. Wyjścia są dwa: albo musimy być ostrożniejsi, albo musimy się nauczyć wzoru, 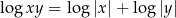 , który jest prawdziwy o ile tylko
, który jest prawdziwy o ile tylko 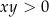 (co na ogół sprawdzamy wyznaczając dziedzinę równania).
(co na ogół sprawdzamy wyznaczając dziedzinę równania).
Podstawianie Podstawianie w równaniach i nierównościach to jedna z najpotężniejszych metod ich rozwiązywania, jednak posługiwanie się tą metodą wymaga odrobiny wprawy. Zwykle sami musimy wymyślić za co należy podstawić, żeby otrzymać prostsze równanie/nierówność.
Najpopularniejszy szkolny motyw z podstawianiem, to równania i nierówności dwukwadratowe. Są to równania/nierówności, w których niewiadoma występuje w wyrażeniu postaci
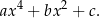
Podstawiając w tym równaniu 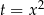 sprowadzamy sytuację do zwykłego równania/nierówności kwadratowej. No prawie zwykłego, bo
sprowadzamy sytuację do zwykłego równania/nierówności kwadratowej. No prawie zwykłego, bo 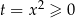 , więc mamy mocno okrojoną dziedzinę.
, więc mamy mocno okrojoną dziedzinę.
Rozwiążmy nierówność 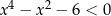 .
.
Podstawiamy 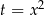 i mamy nierówność
i mamy nierówność
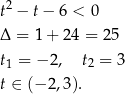
Przypominamy sobie jednak, że interesują nas tylko nieujemne rozwiązania, więc mamy 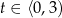 . Daje to nam nierówność
. Daje to nam nierówność
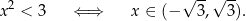
Inne popularne przykłady podstawień to podstawienia za funkcje trygonometryczne,
wykładnicze lub logarytmiczne.
Rozwiążmy równanie 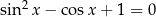 .
.
Podstawiamy 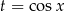 .
.
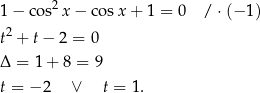
Ze względu na podstawienie 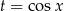 dziedziną naszego równania kwadratowego jest przedział
dziedziną naszego równania kwadratowego jest przedział 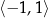 (zbiór wartości funkcji cosinus), więc jedyny pierwiastek to
(zbiór wartości funkcji cosinus), więc jedyny pierwiastek to 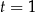 . Stąd
. Stąd 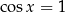 , czyli
, czyli 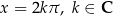 .
.

