/Szkoła średnia/Liczby/Oś liczbowa/Odległość punktów

Zadanie nr 1771483

Dodaj do ulubionych
Dodaj do rozwiązanych

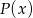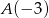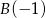Wyznacz algebraicznie zbiór tych wszystkich punktów P (x) osi liczbowej, których suma odległości od punktów A(− 3) oraz B (− 1) jest mniejsza od 5.

Rozwiązanie

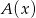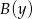Odległość dwóch punktów A (x ) i B (y) osi liczbowej to liczba 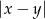|x − y| . Szukamy zatem liczb 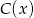C (x) o własności

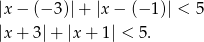
|x− (− 3)|+ |x − (− 1)| < 5 |x+ 3|+ |x + 1| < 5.

Rozwiązujemy to standardowo, rozbijając na przypadki

( | − (x + 3)− (x + 1) < 5 dla x < − 3, { | x + 3 − (x + 1) < 5 dla − 3 ≤ x < −1, ( x + 3 + x + 1 < 5 dla − 1 ≤ x, ( |{ − 2x − 4 < 5 dla x < − 3, 2 < 5 dla − 3 ≤ x < − 1, |( 2x + 4 < 5 dla − 1 ≤ x, ( 9 |{ − 2 < x dla x < − 3, 2 < 5 dla − 3 ≤ x < − 1, |( 1 x < 2 dla − 1 ≤ x,

Otrzymujemy stąd rozwiązanie

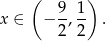
( 9 1 ) x ∈ − -,-- . 2 2

 
Odpowiedź: ( ) x ∈ − 9, 1 2 2

Wersja PDF