/Szkoła średnia/Liczby/Oś liczbowa/Odległość punktów

Zadanie nr 7097250

Dodaj do ulubionych
Dodaj do rozwiązanych

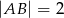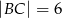Wiadomo, że |AB | = 2 i |BC | = 6 . Znajdź warunek, jaki musi spełniać odległość 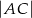|AC | , aby punkty 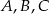A ,B,C były współliniowe.

Rozwiązanie

Wszystkie punkty mają być współliniowe, więc zastanówmy gdzie mogą się znajdować względem siebie.

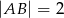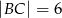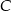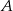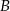Ponieważ |AB | = 2 , a |BC | = 6 , więc punkt C nie może znajdować się między punktami A i B . Zatem punkt 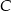C musi znajdować się na prawo lub na lewo od punktu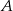 A

Po pierwsze możemy mieć następujący układ

PIC

Wówczas otrzymujemy równanie

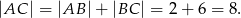
|AC | = |AB | + |BC | = 2+ 6 = 8.

Drugi możliwy układ to

PIC

Wówczas otrzymujemy równanie

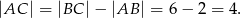
|AC | = |BC |− |AB | = 6− 2 = 4.

 
Odpowiedź: 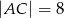|AC | = 8 lub |AC | = 4

Wersja PDF