Zadanie nr 9854876
Niech 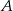 będzie zbiorem wszystkich liczb
będzie zbiorem wszystkich liczb  , które spełniają równość
, które spełniają równość 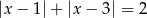 . Niech
. Niech 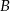 będzie zbiorem wszystkich punktów na osi liczbowej, których suma odległości od punktów 4 i 6 jest niewiększa niż 4. Zaznacz na osi liczbowej zbiory
będzie zbiorem wszystkich punktów na osi liczbowej, których suma odległości od punktów 4 i 6 jest niewiększa niż 4. Zaznacz na osi liczbowej zbiory 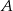 i
i 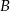 oraz wszystkie punkty, które należą jednocześnie do
oraz wszystkie punkty, które należą jednocześnie do 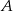 i do
i do 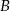 .
.
Rozwiązanie
W rozwiązaniu będziemy korzystać z interpretacji liczby
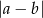
jako odległości na osi liczb  i
i 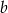 .
.
Równość 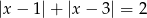 spełniają punkty, których suma odległości od liczb 1 i 3 jest równa 2. Ponieważ przedział
spełniają punkty, których suma odległości od liczb 1 i 3 jest równa 2. Ponieważ przedział 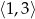 ma dokładnie długość 2, ten warunek spełniają wszystkie liczby z tego przedziału. Z drugiej strony, żadna liczba spoza tego przedziału nie może spełniać tego warunku, bo jej odległość do jednej z liczb 1 lub 3 musi być większa od 2. zatem
ma dokładnie długość 2, ten warunek spełniają wszystkie liczby z tego przedziału. Z drugiej strony, żadna liczba spoza tego przedziału nie może spełniać tego warunku, bo jej odległość do jednej z liczb 1 lub 3 musi być większa od 2. zatem 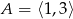 .
.
Podobnie rozszyfrowujemy zbiór 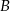 : przedział
: przedział 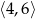 ma długość 2, więc punkty, których suma odległości od końców tego przedziału jest
ma długość 2, więc punkty, których suma odległości od końców tego przedziału jest 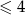 muszą być albo w tym przedziale, albo być w odległości niewiększej niż 1 od jednego z jego końców (bo wtedy suma odległości od końców będzie
muszą być albo w tym przedziale, albo być w odległości niewiększej niż 1 od jednego z jego końców (bo wtedy suma odległości od końców będzie 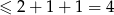 ). Zatem
). Zatem 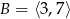 .
.
Zbiory 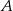 i
i 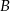 mogliśmy też wyznaczyć czysto rachunkowo. Wystarczy w tym celu rozwiązać równanie i nierówność
mogliśmy też wyznaczyć czysto rachunkowo. Wystarczy w tym celu rozwiązać równanie i nierówność
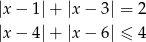
przez standardowe rozbijanie na przypadki.
Jeżeli już wiemy czym są zbiory 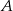 i
i 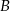 bez trudu wykonujemy obrazek.
bez trudu wykonujemy obrazek.

Z obrazka widać, że 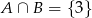 .
.

