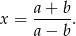Zadanie nr 2973126
Rozwiąż równanie 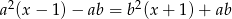 z parametrami
z parametrami  i
i  .
.
Rozwiązanie
Liczymy
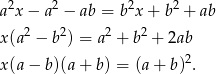
Jeżeli 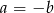 to mamy równanie
to mamy równanie 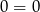 , które spełnia każda liczba rzeczywista. Jeżeli
, które spełnia każda liczba rzeczywista. Jeżeli 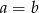 i
i 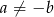 to mamy sprzeczną równość
to mamy sprzeczną równość 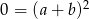 . Jeżeli natomiast
. Jeżeli natomiast 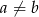 i
i 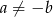 to mamy jedno rozwiązanie
to mamy jedno rozwiązanie
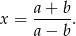
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 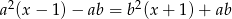 z parametrami
z parametrami  i
i 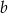 .
.
Liczymy
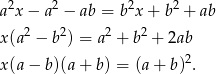
Jeżeli 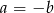 to mamy równanie
to mamy równanie 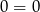 , które spełnia każda liczba rzeczywista. Jeżeli
, które spełnia każda liczba rzeczywista. Jeżeli 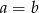 i
i 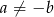 to mamy sprzeczną równość
to mamy sprzeczną równość 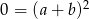 . Jeżeli natomiast
. Jeżeli natomiast 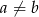 i
i 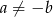 to mamy jedno rozwiązanie
to mamy jedno rozwiązanie