/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt

Zadanie nr 1773517

Dodaj do ulubionych
Dodaj do rozwiązanych

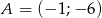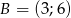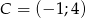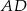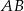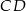Punkty o współrzędnych A = (− 1;− 6) , B = (3;6 ) , C = (−1 ;4) są wierzchołkami trapezu. Ramię trapezu AD jest prostopadłe do podstaw AB i CD . Oblicz współrzędne punktu 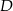D oraz pole powierzchni tego trapezu.

Rozwiązanie

Rozpoczynamy od schematycznego rysunku.

PIC

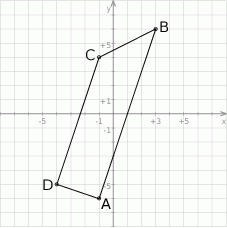
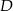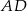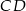Współrzędne punktu D wyznaczymy pisząc równania prostych AD i CD – pierwsza z nich jest prostopadła, a druga równoległa do 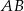AB . Zanim to jednak zrobimy napiszmy równanie prostej 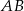AB (potrzebny nam jest jej współczynnik kierunkowy).

Szukamy prostej w postaci 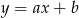y = ax+ b i podstawiamy współrzędne punktów 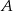A i B .

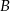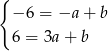
{ − 6 = −a + b 6 = 3a+ b

Odejmując od drugiego równania pierwsze mamy 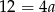12 = 4a , czyli 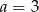a = 3 . No i dalej możemy nie liczyć, bo potrzebny nam był tylko współczynnik kierunkowy.

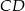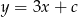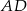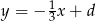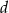W takim razie prosta CD ma postać y = 3x + c , a prosta AD postać 1 y = − 3x + d . Współczynniki c i d wyznaczamy podstawiając współrzędne odpowiednio punktów 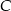C i A .

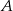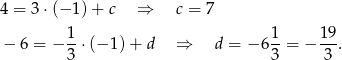
4 = 3⋅ (− 1)+ c ⇒ c = 7 1- 1- 19- − 6 = − 3 ⋅(− 1)+ d ⇒ d = − 6 3 = − 3 .

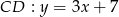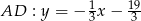Pozostało znaleźć punkt wspólny prostych CD : y = 3x + 7 i AD : y = − 1x − 19 3 3 .

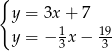
{ y = 3x + 7 1 19 y = − 3 x− 3

Porównując y -ki mamy

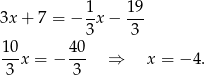
1 19 3x + 7 = − 3x − -3- 10-x = − 40- ⇒ x = − 4. 3 3

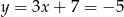Zatem y = 3x + 7 = − 5 i D = (− 4,− 5) .

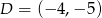Aby obliczyć pole obliczamy długości podstaw i wysokości trapezu.

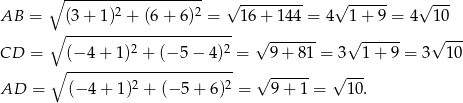
∘ ------------------- √ --------- √ ------ √ --- AB = (3 + 1)2 + (6 + 6)2 = 16 + 14 4 = 4 1 + 9 = 4 10 ∘ ----------------------- √ ------- √ ------ √ --- CD = (− 4 + 1)2 + (− 5 − 4)2 = 9 + 81 = 3 1+ 9 = 3 10 ∘ ----------------------- 2 2 √ ------ √ --- AD = (− 4+ 1 ) + (− 5 + 6) = 9 + 1 = 10.

Pole trapezu jest więc równe

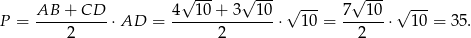
√ --- √ --- √ --- AB + CD 4 1 0+ 3 10 √ --- 7 10 √ --- P = ----------⋅AD = -------------- ⋅ 10 = ------⋅ 10 = 35 . 2 2 2

 
Odpowiedź: 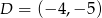D = (− 4,− 5) , pole: 35.

Wersja PDF