Zadanie nr 1908686
Punkt 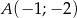 jest wierzchołkiem rombu, którego jeden z boków zawiera się w prostej
jest wierzchołkiem rombu, którego jeden z boków zawiera się w prostej 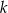 o równaniu
o równaniu 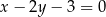 . Środkiem symetrii tego rombu jest punkt
. Środkiem symetrii tego rombu jest punkt 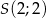 . Oblicz współrzędne pozostałych wierzchołków rombu i oblicz jego pole.
. Oblicz współrzędne pozostałych wierzchołków rombu i oblicz jego pole.
Rozwiązanie
Zaczynamy oczywiście od schematycznego rysunku.
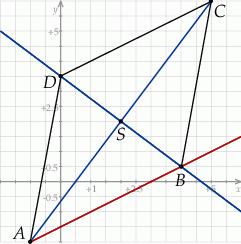
Od razu zauważamy, że punkt 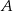 leży na podanej prostej. Od ręki możemy wyznaczyć współrzędne punktu
leży na podanej prostej. Od ręki możemy wyznaczyć współrzędne punktu 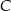 (bo
(bo 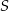 jest środkiem odcinka
jest środkiem odcinka 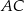 ). Mamy
). Mamy
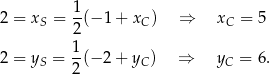
Zatem 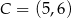 . Co do kolejnych wierzchołków, to jest kilka możliwości, ale najprościej jest skorzystać z tego, że przekątne rombu są prostopadłe. Zatem możemy łatwo napsać równanie przekątnej
. Co do kolejnych wierzchołków, to jest kilka możliwości, ale najprościej jest skorzystać z tego, że przekątne rombu są prostopadłe. Zatem możemy łatwo napsać równanie przekątnej 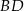 – jest to prosta przechodząca przez
– jest to prosta przechodząca przez 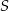 i prostopadła do prostej
i prostopadła do prostej 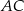 . Skorzystamy z niezwykle wygodnego wzoru na równanie prostej przechodzącej przez punkt
. Skorzystamy z niezwykle wygodnego wzoru na równanie prostej przechodzącej przez punkt 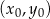 i prostopadłej do wektora
i prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/1908686/HzadR11x.gif)
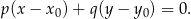
W naszej sytuacji mamy 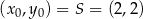 i
i ![→ → v = AC = [6,8]](https://img.zadania.info/zad/1908686/HzadR14x.gif) . Zatem prosta
. Zatem prosta 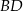 ma równanie
ma równanie
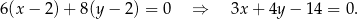
Przecięcie tej prostej z podaną prostą to dokładnie punkt 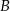 . Aby go znaleźć podstawmy
. Aby go znaleźć podstawmy 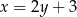 do powyższego równania
do powyższego równania
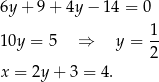
Zatem 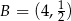 . Punkt
. Punkt 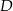 wyznaczamy pdobnie jak wcześniej wyznaczyliśmy punkt
wyznaczamy pdobnie jak wcześniej wyznaczyliśmy punkt 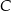 .
.
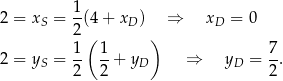
Zatem 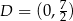 .
.
Pozostało obliczyć pole. Najprościej to zrobić ze wzoru
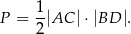
Już wcześniej zauważyliśmy, że ![AC = [6,8]](https://img.zadania.info/zad/1908686/HzadR26x.gif) , zatem
, zatem
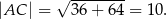
Podobnie,
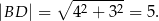
Zatem
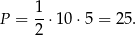
Odpowiedź: 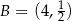 ,
, 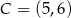 ,
, 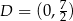 , pole: 25
, pole: 25

