/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt

Zadanie nr 3663878

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane są punkty 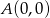A (0,0) i B(4,2) .

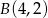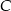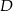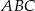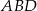  • Znajdź takie punkty C i D aby trójkąty ABC i ABD były równoboczne.
  • Znajdź równanie okręgu wpisanego w romb ABCD .
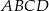  • Oblicz pole figury, którą otrzymamy po usunięciu z rombu ABCD wnętrza wpisanego w niego koła.

Rozwiązanie

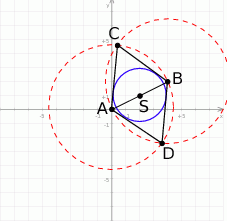
Możemy na początku naszkicować sobie opisaną sytuację.

PIC

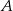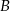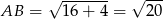  • Szukane punkty C i D możemy wyznaczyć na różne sposoby, my zrobimy to szukając punktów wspólnych okręgów o środkach w A i B i promieniu √ ------- √ --- AB = 16 + 4 = 20 .
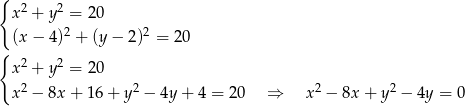
    { 2 2 x + y = 20 (x − 4)2 + (y − 2)2 = 2 0 { x 2 + y2 = 20 x 2 − 8x + 1 6+ y2 − 4y+ 4 = 20 ⇒ x 2 − 8x + y2 − 4y = 0

    Odejmujemy teraz od pierwszego równania drugie i mamy

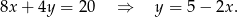
    8x + 4y = 20 ⇒ y = 5− 2x.

    Tę wartość podstawiamy do pierwszego równania.

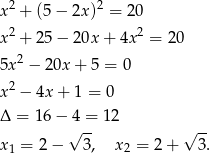
    2 2 x + (5 − 2x) = 20 x2 + 25 − 20x + 4x2 = 20 5x 2 − 20x + 5 = 0 2 x − 4x + 1 = 0 Δ = 16 − 4 = 12 √ -- √ -- x1 = 2− 3, x2 = 2 + 3.

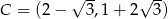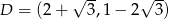    Daje to nam punkty √ -- √ -- C = (2 − 3,1 + 2 3 ) i D = (2+ √ 3,1 − 2√ 3) .  
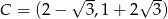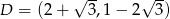
    Odpowiedź: √ -- √ -- C = (2− 3,1+ 2 3) i √ -- √ -- D = (2 + 3,1 − 2 3)

  • Środkiem szukanego okręgu jest środek odcinka 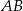AB , czyli punkt 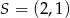S = (2,1 ) . Promień tego okręgu możemy łatwo wyliczyć ze wzoru na pole rombu opisanego na okręgu 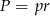P = pr , gdzie 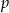p jest połową obwodu (robimy to w ten sposób, bo pole rombu i tak będzie nam potrzebne w następnym podpunkcie).

    Wcześniej już policzyliśmy, że 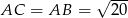√ --- AC = AB = 20 zatem ze wzoru na pole trójkąta równobocznego mamy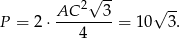

    √ -- AC 2 3 √ -- P = 2⋅ --------= 10 3. 4

    Wyliczamy teraz promień okręgu wpisanego

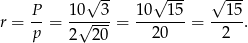
    √ -- √ --- √ --- P 10 3 10 1 5 1 5 r = p-= -√----= --20--- = --2--. 2 20

    Zatem interesujący nas okrąg ma równanie

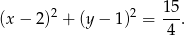
    2 2 15- (x − 2) + (y− 1) = 4 .

     
    Odpowiedź: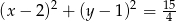 (x − 2)2 + (y − 1)2 = 154

  • Wiemy już, że pole rombu jest równe 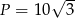√ -- P = 10 3 . Pole okręgu wpisanego jest równe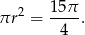
    2 15π πr = ----. 4

    Zatem interesujące nas pole jest równe

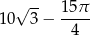
    √ -- 15π- 10 3− 4

     
    Odpowiedź: √ -- 15π 10 3 − 4

Wersja PDF