/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt

Zadanie nr 5030923

Dodaj do ulubionych
Dodaj do rozwiązanych

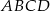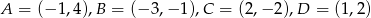Dany jest czworokąt ABCD , gdzie A = (− 1,4 ),B = (− 3,− 1),C = (2,− 2),D = (1,2) .

  • Oblicz pole czworokąta ABCD .
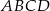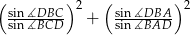  • Oblicz wartość wyrażenia ( sin-∡DBC-)2 ( sin∡DBA--)2 sin ∡BCD + sin∡BAD .

Rozwiązanie

Rozpoczynamy od naszkicowania czworokąta.

PIC

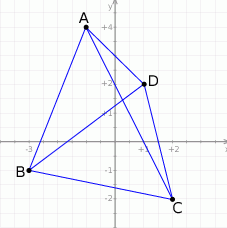
  • Pole czworokąta 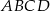ABCD obliczymy jako sumę pól trójkątów 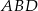ABD i CDB .

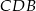    Sposób I

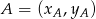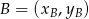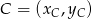    Korzystamy ze wzoru na pole trójkąta o wierzchołkach A = (xA ,yA) , B = (xB,yB) i C = (xC ,yC) .

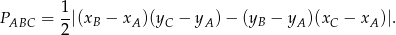
    1- PABC = 2|(xB − xA )(yC − yA )− (yB − yA)(xC − xA)|.

    Mamy zatem

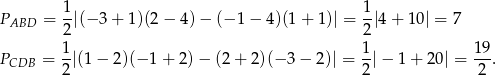
    P = 1-|(− 3 + 1)(2 − 4) − (− 1 − 4)(1 + 1)| = 1-|4 + 1 0| = 7 ABD 2 2 1- 1- 1-9 PCDB = 2 |(1 − 2)(− 1 + 2) − (2 + 2)(− 3 − 2)| = 2 |− 1 + 20| = 2 .

    Zatem

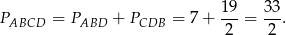
    19 33 PABCD = PABD + PCDB = 7 + ---= ---. 2 2

    Sposób II

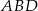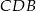    Jeżeli nie chcemy korzystać z gotowego wzoru na pole to możemy obliczyć pola trójkątów ABD i CDB wprost. Liczymy najpierw długość odcinka DB .

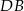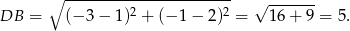
    ∘ ----------------------- √ ------- DB = (−3 − 1 )2 + (− 1 − 2)2 = 1 6+ 9 = 5.

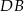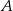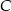    Napiszemy teraz równanie prostej DB i policzymy odległości punktów A i C od tej prostej (czyli długości wysokości trójkątów 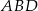ABD i CDB ).

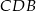    Szukamy prostej postaci 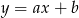y = ax + b i podstawiamy współrzędne punktów 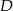D i B .

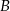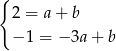
    { 2 = a+ b − 1 = −3a + b

    Odejmując od pierwszego równania drugie mamy 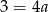3 = 4a , czyli 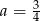a = 34 . Zatem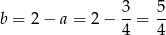

    b = 2 − a = 2− 3-= 5- 4 4

    i prosta 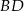BD mam równanie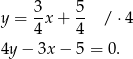

    3 5 y = -x + -- / ⋅4 4 4 4y− 3x− 5 = 0.

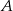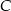    Liczymy teraz odległości punktów A i C od tej prostej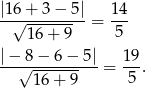

    |1√6+-3-−-5-|= 14- 1 6+ 9 5 |− 8 − 6 − 5| 19 --√-----------= --. 16 + 9 5

    Stąd

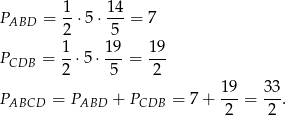
    1 14 PABD = -⋅ 5⋅ ---= 7 2 5 P = 1-⋅5 ⋅ 1-9 = 19 CDB 2 5 2 19 33 PABCD = PABD + PCDB = 7 + -2-= -2-.

     
    Odpowiedź: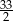 33 2

  • Liczenie sinusów w układzie współrzędnych to udręka, ale dzięki twierdzeniu sinusów możemy zamienić sinusy na długości odcinków. Patrząc na trójkąty 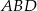ABD i CDB mamy
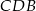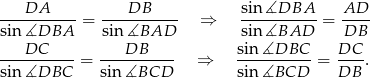
    DA DB sin∡DBA AD -----------= ----------- ⇒ -----------= ---- sin ∡DBA sin ∡BAD sin∡BAD DB ----DC-----= ---DB------ ⇒ sin-∡DBC----= DC--. sin ∡DBC sin∡BCD sin ∡BCD DB

    Mamy więc

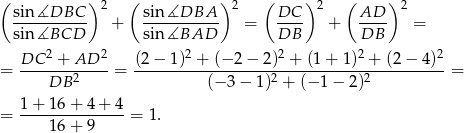
    ( ) 2 ( ) 2 ( )2 ( ) 2 sin∡DBC---- + sin-∡DBA---- = DC-- + AD-- = sin∡BCD sin ∡BAD DB DB DC 2 + AD 2 (2 − 1 )2 + (− 2 − 2)2 + (1 + 1)2 + (2− 4)2 = ------------ = -------------------------------------------= DB 2 (− 3 − 1)2 + (− 1 − 2)2 1 + 16 + 4 + 4 = ----16-+-9-----= 1 .

     
    Odpowiedź: 1

Wersja PDF