/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt

Zadanie nr 5217321

Dodaj do ulubionych
Dodaj do rozwiązanych

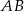Bok AB kwadratu 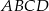ABCD o polu równym 4 jest zawarty w prostej o równaniu 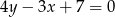4y − 3x + 7 = 0 . Wiadomo ponadto, że wewnątrz tego kwadratu leży początek układu współrzędnych. Napisz równanie prostej zawierającej bok 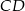CD tego kwadratu.

Rozwiązanie

Szkicujemy opisaną sytuacje – aby naszkicować daną prostą zgadujemy dwa należące do niej punkty. Takimi punktami są np. 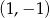(1,− 1) i (− 3,− 4) .

PIC

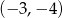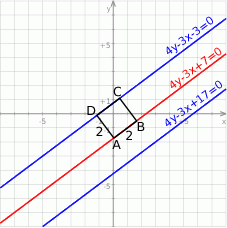
Wiemy, że bok kwadratu 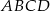ABCD ma długość 2, więc szukana prosta 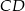CD musi być równoległa do 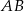AB i odległa od 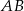AB o 2. Jest to więc zbiór punktów spełniających równanie (korzystamy ze wzoru na odległość punktu od prostej)

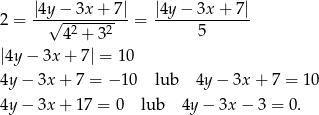
|4y − 3x+ 7| |4y − 3x + 7| 2 = --√--2----2--= ------------- 4 + 3 5 |4y − 3x + 7| = 10 4y − 3x + 7 = − 10 lub 4y − 3x + 7 = 10 4y − 3x + 1 7 = 0 lub 4y − 3x − 3 = 0.

Otrzymaliśmy dwie proste, bo są dwie proste odległe od danej prostej o 2: jedna poniżej 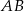AB i jedna powyżej.

Teraz pozostało skorzystać z informacji o tym, że kwadrat 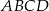ABCD ma zawierać początek układu współrzędnych – prosta 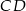CD musi więc mieć równanie 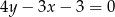4y − 3x − 3 = 0 (bo leży ona powyżej prostej AB ).  
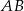Odpowiedź: 4y − 3x − 3 = 0

Wersja PDF