Zadanie nr 5473234
Dane są punkty 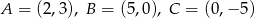 .
.
- Uzasadnij, że proste
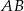 i
i 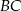 są prostopadłe.
są prostopadłe. - Wyznacz współrzędne takiego punktu
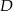 , dla którego czworokąt
, dla którego czworokąt 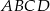 jest prostokątem.
jest prostokątem. - Oblicz pole prostokąta
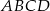 .
.
Rozwiązanie
Możemy zacząć od szkicowego rysunku.
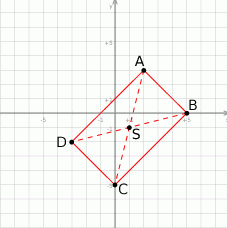
-
Sposób I
Napiszemy równania prostych
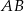 i
i 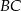 i sprawdzimy, że są prostopadłe. Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty
i sprawdzimy, że są prostopadłe. Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty 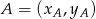 i
i 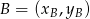 :
: 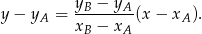
Mamy zatem
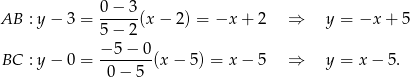
Ponieważ iloczyn współczynników kierunkowych otrzymanych prostych jest równy -1, proste te są prostopadłe.
Sposób II
Zamiast pisać równania prostych, mogliśmy skorzystać z twierdzenia Pitagorasa: wystarczy sprawdzić, czy
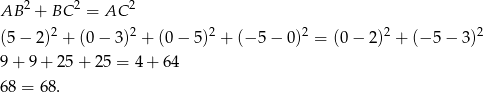
Otrzymaliśmy prawdziwą równość co dowodzi, że trójkąt
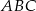 jest prostokątny.
jest prostokątny. -
Sposób I
Jeżeli poprzedni podpunkt rozwiązywaliśmy pisząc równania prostych to wiemy jakie mają być współczynniki kierunkowe boków prostokąta, więc łatwo napisać równania prostych
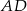 i
i 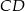 . Prosta
. Prosta 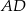 jest postaci
jest postaci 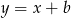 . Ponieważ ma niej leżeć punkt
. Ponieważ ma niej leżeć punkt 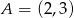 mamy
mamy 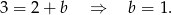
Podobnie wyznaczamy równanie prostej
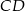 . Musi ono mieć postać
. Musi ono mieć postać 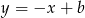 . Podstawiając współrzędne punktu
. Podstawiając współrzędne punktu 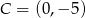 mamy
mamy 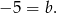
Pozostało znaleźć punkt wspólny
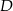 tych dwóch prostych.
tych dwóch prostych. 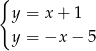
Dodając te dwa równania stronami mamy
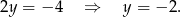
Stąd
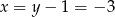 i
i 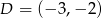 .
. Sposób II
Ponieważ przekątne prostokąta dzielą się na połowy, łatwo jest wyliczyć ich punkt wspólny
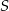 : jest to po prostu środek odcinka
: jest to po prostu środek odcinka 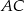 .
. 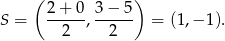
Z drugiej strony, musi to być środek odcinka o końcach
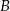 i
i 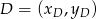 , czyli
, czyli 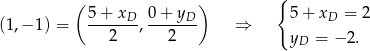
Zatem
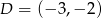 .
.
Odpowiedź: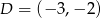
- Liczymy długości boków prostokąta.
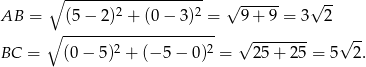
Zatem pole jest równe
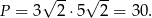
Odpowiedź: 30

