/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt

Zadanie nr 5764838

Dodaj do ulubionych
Dodaj do rozwiązanych

Wierzchołki czworokąta 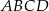ABCD mają współrzędne: 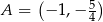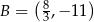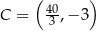( 5) A = − 1,− 4 , ( ) B = 8,− 11 3 , ( ) C = 40,− 3 3 i ( ) D = 5, 13 4 .

  • Wykaż, że czworokąt 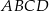ABCD jest trapezem równoramiennym, w który można wpisać okrąg.
  • Wyznacz współrzędne punktu styczności okręgu wpisanego w czworokąt 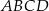ABCD z prostą CD .

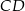Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

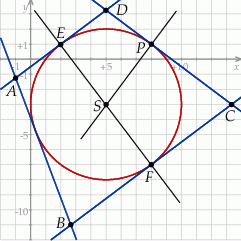
  • Zauważmy najpierw
    [ ] [ ] −→ 13 5 9 3 AD = 5+ 1,-4-+ 4- = 6,2- = 2-⋅[4,3] [ ] [ ] −→ 40- 8- 32- 8- BC = 3 − 3,− 3+ 11 = 3 ,8 = 3 ⋅[4,3].

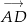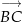    To oznacza, że wektory −→ AD i −→ BC są równoległe, czyli czworokąt 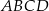ABCD rzeczywiście jest trapezem. Ponadto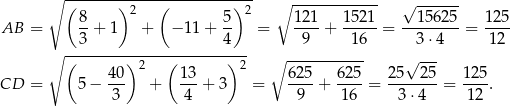

    ∘ (-------)2---(---------)-2 ∘ ------------ √ ------ 8- 5- 121- 1521- --15625- 125- AB = 3 + 1 + − 11+ 4 = 9 + 16 = 3⋅4 = 12 ∘ -------------------------- ∘ ----------- √ --- ( 40 )2 ( 13 )2 625 625 25 25 125 CD = 5 − --- + ---+ 3 = ----+ ----= -------= ----. 3 4 9 1 6 3 ⋅4 12

    To oznacza, że 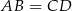AB = CD , więc rzeczywiście mamy do czynienia z trapezem równoramiennym. Co więcej,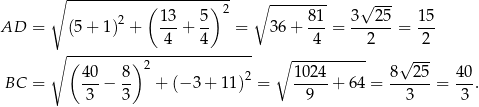

    ∘ -----------(--------)2- ∘ -------- √ --- 2 13- 5- 81- 3--25- 15- AD = (5+ 1) + 4 + 4 = 36+ 4 = 2 = 2 ∘ -------------------------- ∘ ----------- √ --- ( 40 8 )2 2 1024 8 25 4 0 BC = ---− -- + (− 3 + 11) = -----+ 64 = ------ = ---. 3 3 9 3 3

    Stąd

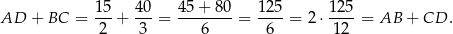
    AD + BC = 1-5+ 40-= 45-+-80-= 125-= 2⋅ 125-= AB + CD . 2 3 6 6 12

    To oznacza, że w trapez ABCD można wpisać okrąg.

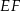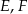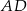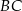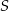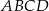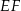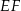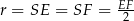  • Trapez równoramienny ma oś symetrii EF przechodzącą przez środki E ,F podstaw AD i BC . To oznacza, że środek S okręgu wpisanego w trapez ABCD leży na odcinku EF . Ponadto EF jest średnicą tego okręgu, więc promień r tego okręgu jest równy r = SE = SF = EF- 2 .
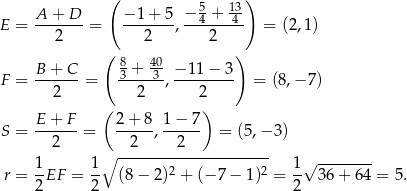
    ( 5 13) E = A--+-D- = −-1-+-5 , −-4-+-4- = (2,1 ) 2 2 2 ( ) B-+--C 83-+-403- −1-1−--3- F = 2 = 2 , 2 = (8,− 7) ( ) E-+--F 2-+-8- 1-−-7- S = 2 = 2 , 2 = (5,− 3) ∘ --------------------- √ -------- r = 1-EF = 1- (8− 2)2 + (−7 − 1 )2 = 1- 36 + 6 4 = 5. 2 2 2

    To oznacza, że okrąg wpisany w trapez 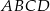ABCD ma równanie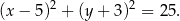

    (x − 5)2 + (y + 3)2 = 25.

    Napiszemy teraz równanie prostej 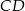CD . Szukamy prostej w postaci 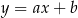y = ax + b i podstawiamy współrzędne punktów 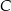C i D .

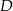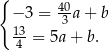
    { −3 = 430a+ b 13 4 = 5a + b.

    Odejmujemy od pierwszego równania drugie i mamy

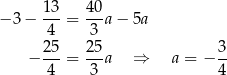
    13 40 − 3− ---= --a − 5a 4 3 − 25-= 25a ⇒ a = − 3- 4 3 4

    Stąd 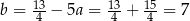b = 13 − 5a = 13+ 15= 7 4 4 4 i prosta 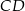CD ma równanie 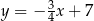3 y = − 4x + 7 . Szukany punkt styczności 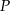P to punkt wspólny tej prostej i okręgu wpisanego w czworokąt 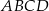ABCD , więc podstawiamy 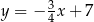y = − 34x + 7 do równania okręgu.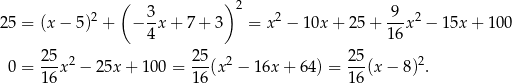

    ( ) 2 25 = (x− 5)2 + − 3x + 7 + 3 = x2 − 10x + 25 + 9-x2 − 15x + 1 00 4 16 25 2 25 2 25 2 0 = --x − 2 5x+ 100 = --(x − 16x + 64) = ---(x− 8) . 16 16 16

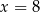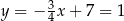    Zatem x = 8 , y = − 3x + 7 = 1 4 i P = (8,1) .  
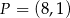    Odpowiedź: (8,1)

Wersja PDF