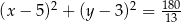Zadanie nr 6113516
Punkt 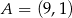 jest wierzchołkiem rombu
jest wierzchołkiem rombu 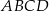 o polu 60. Przekątna
o polu 60. Przekątna 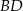 zawiera się w prostej
zawiera się w prostej 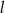 o równaniu
o równaniu 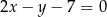 . Wyznacz równanie okręgu wpisanego w ten romb.
. Wyznacz równanie okręgu wpisanego w ten romb.
Rozwiązanie
Zaczynamy oczywiście od schematycznego rysunku.
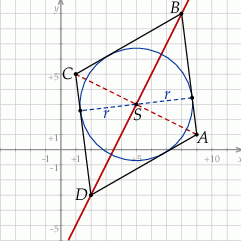
Środkiem okręgu wpisanego w romb jest punkt 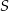 przecięcia się jego przekątnych. Aby go wyznaczyć zacznijmy od napisania równania drugiej przekątnej – jest to prosta postaci
przecięcia się jego przekątnych. Aby go wyznaczyć zacznijmy od napisania równania drugiej przekątnej – jest to prosta postaci 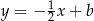 (bo jest prostopadła do
(bo jest prostopadła do  ) i przechodzi przez
) i przechodzi przez  , więc
, więc
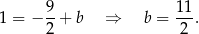
Punkt 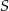 jest punktem wspólnym prostych
jest punktem wspólnym prostych 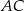 i
i 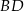 , czyli jego współrzędne są rozwiązaniami układu równań
, czyli jego współrzędne są rozwiązaniami układu równań
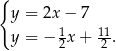
Odejmujemy równania stronami i mamy
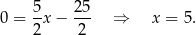
Stąd 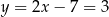 i
i 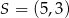 .
.
Średnica okręgu wpisanego w romb jest równa jego wysokości – łatwo ją będzie obliczyć z podanego pola jeżeli tylko będziemy wiedzieli jaka jest długość boku rombu.
Sposób I
Jeżeli 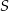 jest środkiem rombu, to łatwo obliczyć długość odcinka
jest środkiem rombu, to łatwo obliczyć długość odcinka 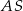 – jest to odległość punktu
– jest to odległość punktu 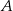 od danej prostej
od danej prostej 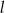 . Mamy zatem
. Mamy zatem
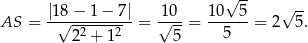
To z kolei pozwala łatwo obliczyć długość odcinka 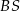 – korzystamy z podanego pola rombu.
– korzystamy z podanego pola rombu.
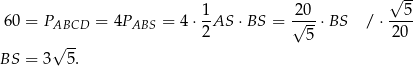
Teraz łatwo obliczyć długość boku rombu – korzystamy tego, że przekątne rombu są prostopadłe
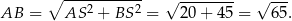
Obliczamy teraz wysokość rombu.
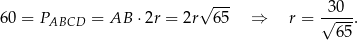
Okrąg wpisany w romb  ma więc równanie
ma więc równanie
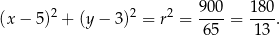
Sposób II
Jeżeli jesteśmy trochę mniej sprytni, to możemy powyznaczać współrzędne wierzchołków rombu. Obliczamy najpierw długość odcinka 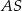 .
.
Tak jak w poprzednim sposobie obliczamy długość odcinka 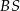 .
.
Wierzchołki  i
i  mają współrzędne postaci
mają współrzędne postaci 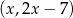 oraz
oraz
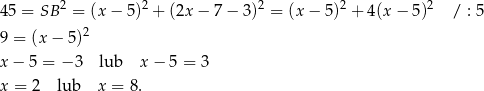
Wybieramy którekolwiek z rozwiąząń i mamy np. 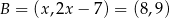 . Stąd
. Stąd
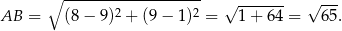
Promień okręgu i jego równanie wyznaczamy tak samo jak w poprzednim sposobie.
Odpowiedź: