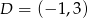Zadanie nr 6433681
Punkty 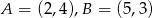 i
i 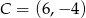 są sąsiednimi wierzchołkami czworokąta
są sąsiednimi wierzchołkami czworokąta 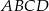 wpisanego w okrąg. Wierzchołek
wpisanego w okrąg. Wierzchołek 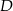 tego czworokąta leży na prostej o równaniu
tego czworokąta leży na prostej o równaniu 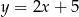 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu  .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
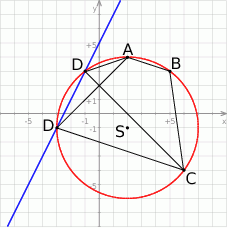
Wyznaczymy najpierw współrzędne środka okręgu opisanego na czworokącie 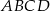 . Punkt ten można wyznaczyć jako punkt wspólny symetralnych odcinków
. Punkt ten można wyznaczyć jako punkt wspólny symetralnych odcinków 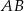 i
i 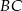 , ale my zrobimy to inaczej – szukamy punktu
, ale my zrobimy to inaczej – szukamy punktu 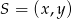 , którego odległości od
, którego odległości od 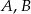 i
i 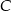 są równe.
są równe.
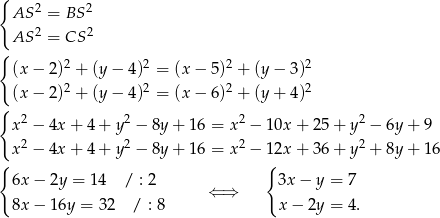
Odejmujemy od pierwszego równania drugie pomnożone przez 3 i mamy
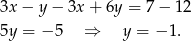
Stąd 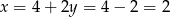 i
i 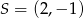 .
.
Teraz szukamy takiego punktu 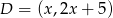 leżącego na danej prostej, dla którego
leżącego na danej prostej, dla którego 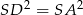 .
.
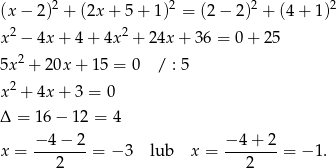
Mamy wtedy 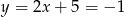 lub
lub 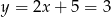 odpowiednio. Są zatem dwa punkty spełniające warunki zadania
odpowiednio. Są zatem dwa punkty spełniające warunki zadania 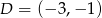 lub
lub 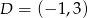 .
.
Odpowiedź: 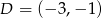 lub
lub