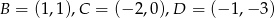Zadanie nr 6700809
Dany jest kwadrat 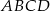 o polu 10 i wierzchołku
o polu 10 i wierzchołku 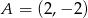 . Przekątna
. Przekątna 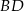 tego kwadratu ma równanie
tego kwadratu ma równanie 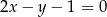 . Oblicz współrzędne pozostałych wierzchołków kwadratu.
. Oblicz współrzędne pozostałych wierzchołków kwadratu.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
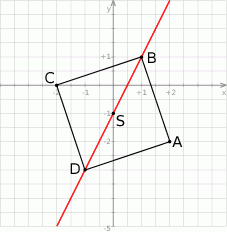
Zaczniemy od wyznaczenia współrzędnych punktów  i
i  . Wiemy, że kwadrat ma pole 10, więc
. Wiemy, że kwadrat ma pole 10, więc 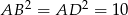 . Wiemy też, że punkty te leżą na prostej
. Wiemy też, że punkty te leżą na prostej 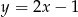 . Szukamy zatem punktów postaci
. Szukamy zatem punktów postaci 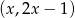 , których kwadrat odległości od
, których kwadrat odległości od 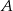 jest równy 10.
jest równy 10.
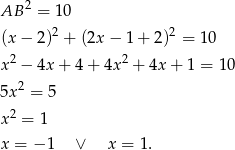
Wtedy odpowiednio 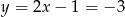 i
i 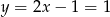 . Zatem
. Zatem 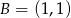 i
i 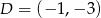 (lub odwrotnie).
(lub odwrotnie).
Łatwo teraz obliczyć współrzędne środka kwadratu 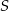 .
.
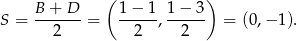
Punkt 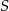 jest też środkiem odcinka
jest też środkiem odcinka 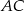 , więc współrzędne punktu
, więc współrzędne punktu 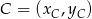 spełniają warunek.
spełniają warunek.
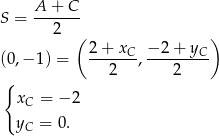
Zatem 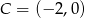 .
.
Odpowiedź: