/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt

Zadanie nr 6780810

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz równanie okręgu wpisanego w deltoid, którego boki są zawarte w prostych o równaniach 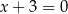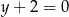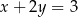x + 3 = 0 , y+ 2 = 0 , x+ 2y = 3 i y + 2x = 2 .

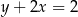Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

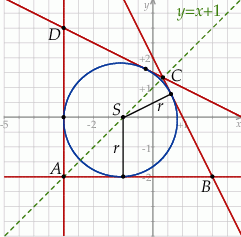
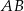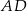Zauważmy, że dwa boki AB i AD deltoidu są równoległe do osi układu współrzędnych, więc bardzo łatwo jest odgadnąć równanie dwusiecznej kąta 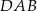DAB : jest to prosta postaci 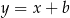y = x + b , która musi przechodzić przez 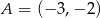A = (− 3,− 2) . Jest to więc prosta 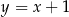y = x+ 1 . Współrzędne środka 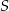S okręgu wpisanego w deltoid mają więc postać 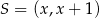S = (x,x+ 1) . 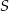Wystarczy teraz wyznaczyć wartość x , dla której odległość punktu S od prostej 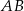AB jest taka sama jak jego odległość od prostej BC .

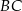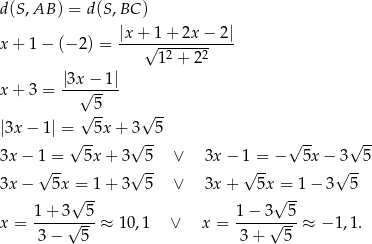
d (S,AB ) = d (S ,BC ) |x+ 1+ 2x− 2| x + 1 − (− 2) = ---√------------ 12 + 22 |3x − 1| x + 3 = --√----- √ 5- √ -- |3x − 1| = 5x + 3 5 √ -- √ -- √ -- √ -- 3x − 1 = 5x + 3 5 ∨ 3x− 1 = − 5x − 3 5 √ -- √ -- √ -- √ -- 3x − 5x√=-1 + 3 5 ∨ 3x+ 5x√=-1 − 3 5 1 + 3 5 1− 3 5 x = -----√---≈ 10,1 ∨ x = ----√----≈ −1 ,1. 3− 5 3 + 5

Z rysunku jest jasne, że pierwsze rozwiązanie daje nam okrąg leżący poza deltoidem, więc mamy

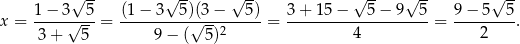
√ -- √ -- √ -- √ -- √ -- √ -- x = 1−--3√--5-= (1−--3--5)√(3-−---5)-= 3+--15−----5−--9--5-= 9−--5--5. 3 + 5 9 − ( 5 )2 4 2

Interesujący nas okrąg ma więc środek

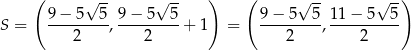
( √ -- √ -- ) ( √ -- √ --) 9-−-5--5- 9−--5--5- 9-−-5--5- 11-−-5--5- S = 2 , 2 + 1 = 2 , 2

i promień

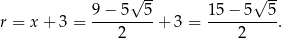
√ -- √ -- r = x+ 3 = 9-−-5--5-+ 3 = 15-−-5--5-. 2 2

Równanie tego okręgu to

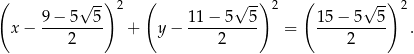
( √ --) 2 ( √ -) 2 ( √ -) 2 9 − 5 5 11− 5 5 15 − 5 5 x − ----2---- + y − ----2----- = ----2----- .

 
Odpowiedź: ( √ -)2 ( √-) 2 ( √-) 2 x − 9−5--5 + y − 11−-5-5- = 15−-5-5 2 2 2

Wersja PDF