Zadanie nr 7508248
Prosta 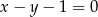 jest osią symetrii pewnego czworokąta wpisanego w okrąg. Punkty
jest osią symetrii pewnego czworokąta wpisanego w okrąg. Punkty 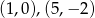 są jego wierzchołkami. Znajdź pozostałe wierzchołki.
są jego wierzchołkami. Znajdź pozostałe wierzchołki.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
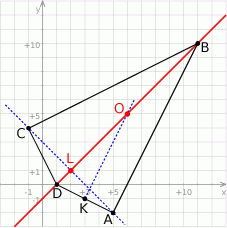
Oznaczmy 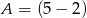 i
i 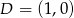 . Rozpocznijmy od wyznaczenia współrzędnych punktu
. Rozpocznijmy od wyznaczenia współrzędnych punktu 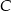 . Jest on symetryczny do punktu
. Jest on symetryczny do punktu 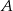 względem podanej prostej. Napiszmy równanie prostej prostopadłej do prostej
względem podanej prostej. Napiszmy równanie prostej prostopadłej do prostej 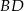 i przechodzącej przez punkt
i przechodzącej przez punkt 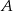 . Szukamy prostej w postaci
. Szukamy prostej w postaci 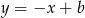 (bo ma być prostopadła do
(bo ma być prostopadła do 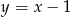 ). Współczynnik
). Współczynnik 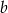 wyznaczmy wstawiając współrzędne punktu
wyznaczmy wstawiając współrzędne punktu 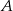 .
.
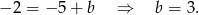
Szukamy teraz punktu przecięcia prostych 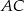 i
i 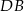 .
.
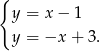
Dodajemy równania stronami i mamy 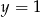 . Stąd
. Stąd 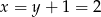 i
i 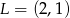 .
.
Punkt 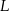 jest środkiem odcinka
jest środkiem odcinka 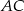 , więc
, więc
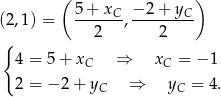
Zatem 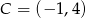 . Współrzędne punktu
. Współrzędne punktu 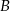 wyznaczymy na dwa sposoby.
wyznaczymy na dwa sposoby.
Sposób I
Wiemy, że czworokącie 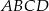 można opisać okrąg – wyznaczymy jego środek
można opisać okrąg – wyznaczymy jego środek 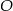 . Mając współrzędne punktu
. Mając współrzędne punktu 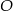 łatwo wyznaczmy współrzędne punktu
łatwo wyznaczmy współrzędne punktu 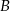 , bo odcinek
, bo odcinek 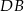 musi być średnicą okręgu opisanego na czworokącie
musi być średnicą okręgu opisanego na czworokącie 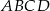 .
.
Punkt 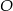 jest punktem wspólnym prostej
jest punktem wspólnym prostej 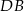 oraz symetralnej odcinka
oraz symetralnej odcinka 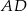 . Napiszemy równanie tej symetralnej. Środkiem odcinka
. Napiszemy równanie tej symetralnej. Środkiem odcinka 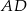 jest punkt
jest punkt
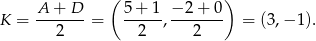
Symetralną odcinka 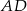 napiszemy korzystając ze wzoru na równanie prostej prostopadłej do wektora
napiszemy korzystając ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/7508248/HzadR35x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 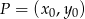
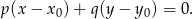
W naszej sytuacji mamy 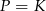 i
i ![→v = −A→D = [−4 ,2]](https://img.zadania.info/zad/7508248/HzadR39x.gif) . Równanie prostej
. Równanie prostej 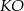 ma więc postać
ma więc postać
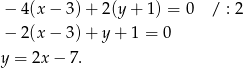
Szukamy teraz punktu wspólnego prostych 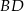 i
i 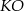 , czyli punktu
, czyli punktu 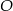 .
.
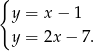
Odejmujemy od drugiego równania pierwsze i mamy 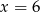 . Stąd
. Stąd 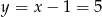 i
i 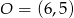 . Pozostało teraz skorzystać z tego, że
. Pozostało teraz skorzystać z tego, że 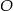 jest środkiem odcinka
jest środkiem odcinka 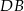 .
.
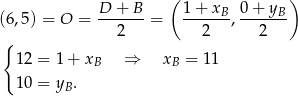
Zatem 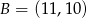 .
.
Sposób II
Zauważmy, że ponieważ 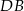 jest średnicą okręgu opisanego na czworokącie
jest średnicą okręgu opisanego na czworokącie 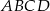 , kąt
, kąt 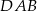 jest prosty. To oznacza, że możemy dość łatwo napisać równanie prostej
jest prosty. To oznacza, że możemy dość łatwo napisać równanie prostej 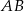 – jest to prosta prostopadła do
– jest to prosta prostopadła do 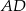 i przechodząca przez
i przechodząca przez 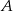 . Jej równanie napiszemy korzystając ze wzoru na równanie prostej prostopadłej do wektora
. Jej równanie napiszemy korzystając ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/7508248/HzadR59x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 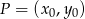
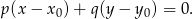
W naszej sytuacji 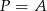 i
i ![→ −→ v = AD = [− 4,2]](https://img.zadania.info/zad/7508248/HzadR63x.gif) . Zatem prosta
. Zatem prosta 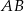 ma równanie
ma równanie
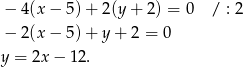
Pozostało teraz znaleźć punkt wspólny prostych 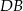 i
i 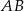 .
.
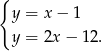
Odejmujemy od drugiego równania pierwsze i mamy 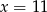 . Stąd
. Stąd 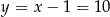 i
i 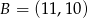 .
.
Odpowiedź: 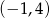 i
i