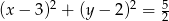/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt

Zadanie nr 8069387

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz równanie okręgu wpisanego w kwadrat 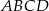ABCD , gdzie 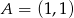A = (1,1) i C = (5,3) .

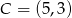Rozwiązanie

Możemy rozpocząć od szkicowego rysunku.

PIC

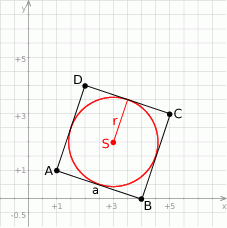
Środkiem okręgu wpisanego w kwadrat jest środek przekątnej 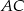AC , czyli punkt

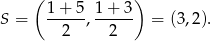
( ) S = 1-+-5, 1-+-3 = (3,2). 2 2

Aby obliczyć jego promień, obliczmy najpierw długość przekątnej 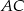AC .

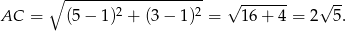
∘ ------------------- 2 2 √ ------- √ -- AC = (5 − 1) + (3 − 1) = 16 + 4 = 2 5.

Jeżeli zatem oznaczymy długość boku kwadratu przez a , to mamy

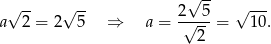
√ -- √ -- √ -- 2--5- √ --- a 2 = 2 5 ⇒ a = √ 2- = 10.

promień r okręgu wpisanego w kwadrat ABCD jest dwa razy krótszy, czyli

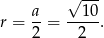
a √ 10- r = --= -----. 2 2

Zatem interesujący nas okrąg ma równanie

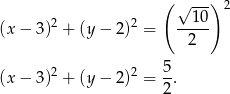
( √ ---) 2 2 2 --1-0 (x − 3) + (y − 2) = 2 2 2 5- (x − 3) + (y − 2) = 2.

 
Odpowiedź: (x − 3)2 + (y − 2)2 = 5 2

Wersja PDF