Zadanie nr 8635514
Wykaż, że punkt o współrzędnych 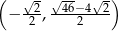 jest wierzchołkiem kwadratu opisanego na okręgu o równaniu
jest wierzchołkiem kwadratu opisanego na okręgu o równaniu
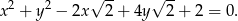
Rozwiązanie
Przekształćmy dane równanie okręgu tak, aby ustalić jaki jest jego środek i promień.
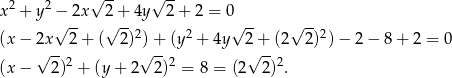
Jest to więc okrąg o środku 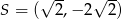 i promieniu
i promieniu 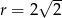 .
.
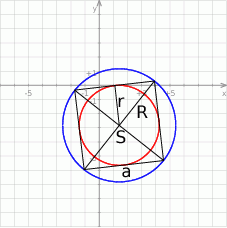
Jeżeli oznaczymy przez  długość boku kwadratu opisanego na tym okręgu, to
długość boku kwadratu opisanego na tym okręgu, to
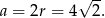
Jeżeli teraz 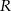 jest promieniem okręgu opisanego na tym kwadracie, to
jest promieniem okręgu opisanego na tym kwadracie, to
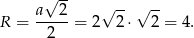
Pozostało teraz sprawdzić, że dany punkt 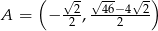 leży w odległości
leży w odległości 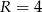 od środka
od środka 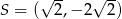 danego okręgu. Liczymy
danego okręgu. Liczymy
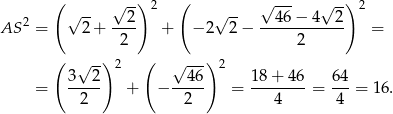
Zatem rzeczywiście 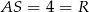 .
.

